| Россия |
Анализ потока управления
Построение отношения обязательного предшествования
Свойства альтов дают возможность использовать их для определения отношения обязательного предшествования. Для этого достаточно для каждой вершины построить максимальный альт, начинающийся в ней, и затем включить эту вершину во множество обязательных предшественников для каждой вершины из этого альта.
После построения отношения обязательного предшествования сводимость графа может быть проверена элементарно - достаточно построить глубинное остовное дерево и проверить, что в любой обратной по отношению к нему дуге конец обязательно предшествует началу.
Луч
Лучом называется фрагмент, который, во-первых, является альтом, а во-вторых, обладает тем свойством, что произвольная его вершина, отличная от начальной и выходной, имеет одного предка и одного потомка, каждый из которых принадлежит лучу. Иными словами, луч - это линейная последовательность вершин.
Легко видеть, что в состав лучей могут входить только деревянные дуги.
Нумерация # называется правильной, если она приписывает вершинам произвольного луча последовательные номера.
Если # - правильная нумерация, а R - максимальный луч, то можно доказать следующие утверждения:
- вершина p является начальной вершиной R тогда и только тогда, когда либо p=start либо #-1(#(p)-1) - выходная вершина некоторого максимального луча
- вершина q является выходной вершиной R тогда и только тогда, когда либо p=stop либо #-1(#(p)+1) - начальная вершина некоторого максимального луча
Легко показать, что нумерации Pre и Post являются правильными.
Выделение лучей
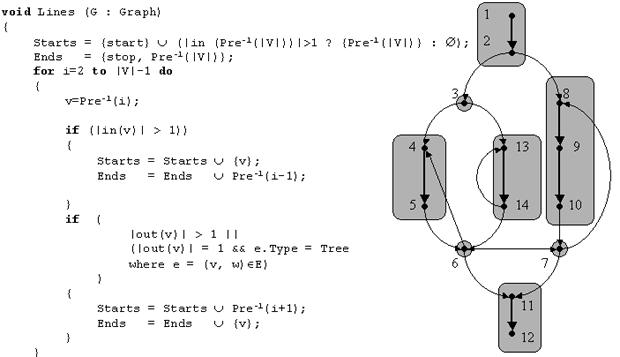
Алгоритм выделения максимальных лучей использует свойства правильных нумераций и элементарное наблюдение, что вершина v является начальной вершиной максимального луча в том случае, если в нее входит более одного ребра, и выходной - если выходит более одного ребра.
Результатом работы алгоритма является два списка Starts и Ends , первый из которых содержит начальные вершины максимальных лучей, а второй - выходные.
Очевидно, что одна вершина является лучом. Таким образом, множество максимальных лучей образует разбиение множества вершин графа. На иллюстрации показано это разбиение.