Линейная оптимизация (поиск решения)
7.2 Пример задачи линейной оптимизации
Для разбора предлагается задача, взятая из учебного пособия "Математическое программирование", авторы Э.Ф.Брыжина и Э.А.Худобина, издательство СПбГИЭА, 1997 год.
Задача: Имеется три вида сырья в количествах 45 ед., 19 ед. и 10 ед. Из этого сырья нужно изготовить продукцию двух видов. Задан расход сырья каждого вида на производство единицы каждого вида продукции и прибыть от единицы продукции (см. таблицу). Требуется найти такой вариант выпуска каждого вида продукции, при котором прибыль будет наибольшей.
Обозначим через  количество единиц продукции первого вида, через
количество единиц продукции первого вида, через  – второго вида. Тогда на выпуск этой продукции будет израсходовано
– второго вида. Тогда на выпуск этой продукции будет израсходовано  ед. сырья первого вида,
ед. сырья первого вида,  ед сырья второго вида и
ед сырья второго вида и 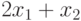 – третьего. Суммарная прибыль составит
– третьего. Суммарная прибыль составит  денежных единиц. Т.к. нельзя израсходовать сырья больше, чем имеется, а суммарная прибыль зависит от количества выпущенной продукции, то получим следующую математическую модель данной задачи.
денежных единиц. Т.к. нельзя израсходовать сырья больше, чем имеется, а суммарная прибыль зависит от количества выпущенной продукции, то получим следующую математическую модель данной задачи.
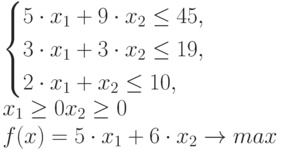 |
( 7.6) |
7.3 Решение в Gnumeric
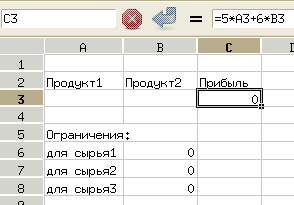
Для решения задачи в ЭТ прежде всего нужно определиться с расположением исходных данных и составить необходимые формулы. Пусть таблица будет скомпонована в соответствии с рис. 7.1.
Количества продукции 1-го и 2-го вида (которые предстоит вычислить) располагаются в ячейках A3 и B3 соответственно. В ячейку C3 записывается формула для вычисления прибыли, в ячейки B6:B8 – формулы для левых частей ограничений (см. математическую модель). Когда решение будет найдено, нули будут заменены какими-то другими значениями.
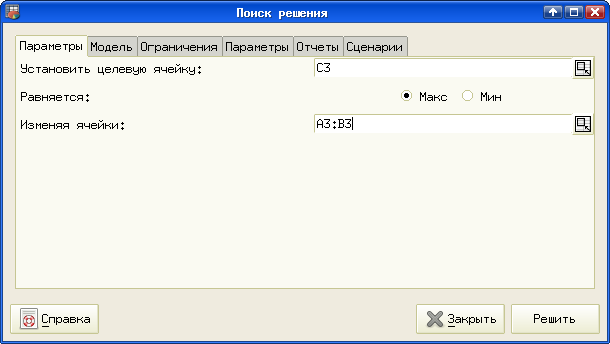
Далее вызываем модуль поиска решения (в главном меню "Сервис/Поиск решения...", рис. 7.2).
В диалоге поиска решения несколько вкладок, и в них потребуется устанавливать значения элементов ввода. На вкладке "Параметры" (рис. 7.2) требуется указать ячейку, содержащую формулу для целевой функции f(x), а также ячейки, в которых должны вычисляться параметры (в нашем случае  и
и  ). Заполним эту вкладку в соответствии с расположением исходных данных. Поскольку требуется найти максимум прибыли, установим переключатель "Равняется:" в позицию "Макс".
). Заполним эту вкладку в соответствии с расположением исходных данных. Поскольку требуется найти максимум прибыли, установим переключатель "Равняется:" в позицию "Макс".
Адреса ячеек, содержащих целевую функцию и значения факторов, можно вписывать вручную, а можно указывать мышью, используя кнопку "свернуть/развернуть диалог" справа от полей ввода.
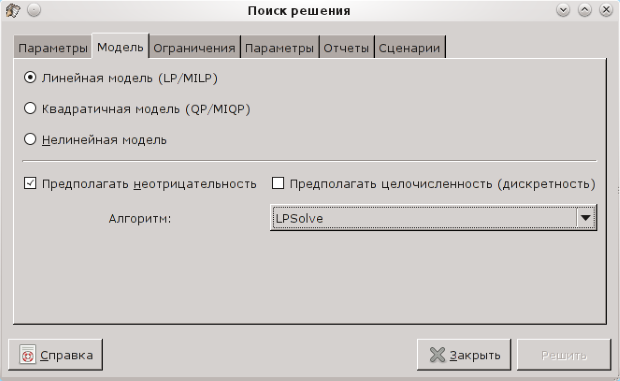
На следующей вкладке ("Модель") устанавливаем значения в соответствии с рис. 7.3. Ключ "Предполагать неотрицательность" как раз и означает, что искать нужно только положительные решения. В самом деле, количество продукции не может быть отрицательным.
Выбор алгоритма и вида модели влияет на результат и саму возможность существования решения, так что для задач линейного программирования нужно использовать установки, показанные на рис. 7.3.
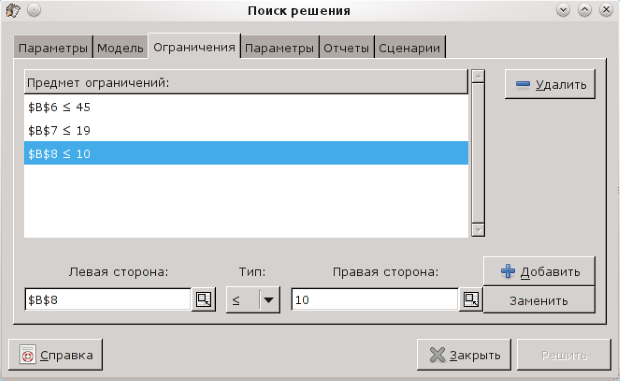
Следующая вкладка ("Ограничения") позволяет задать ограничения для параметров модели. Здесь важно, что левая и правая часть ограничений задаются как адреса ячеек, содержащих формулы и значения. После того, как определены ячейка для левой части и значение для правой части ограничения и выбран знак отношения ("Тип"), нажатием на кнопку "Добавить" условие добавляется (рис. 7.4).
Для правой части ограничений можно использовать как конкретные значения, так и адреса ячеек, содержащих эти значения.
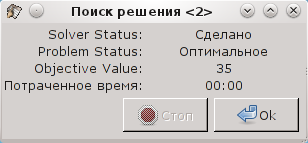
Остальные вкладки не играют существенной роли в решений задачи, поэтому после ввода всех ограничений нажимаем на кнопку "Решить" и получаем сообщение о результате решения (рис. 7.5). Если чего-то не хватает или выбраны неверная модель или алгоритм, выводится соответствующее сообщение об ошибке.
Значение "Objective value" соответствует полученному в результате решения значению целевой функции, а вычисленные значения переменных и результирующие значения ограничений появляются вместо исходных данных на листе таблицы, как показано на рис. 7.6.
Нужно отметить, что результаты полностью соответствуют приведенным в первоисточнике значениям 3 и 10/3.
В качестве эксперимента попробуйте в диалоге настройки модели для этих же исходных данных установить режим "Предполагать целочисленность (дискретность)".