Регрессионный анализ в Gnumeric
6.2 Реализация вычислений на модели
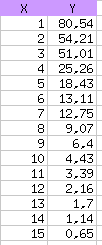
Вычисление параметров линейной регрессии уже рассматривалось в главе "Инструменты Gnumeric для статистиков", поэтому здесь рассмотрим подробнее процесс добавления и настройки параметров линий регрессии на график с экспериментальными данными. В качестве исходных данных используем таблицу, которая уже применялась в главе про статистику при описании инструментов предсказания и регрессии (рис. 6.1).
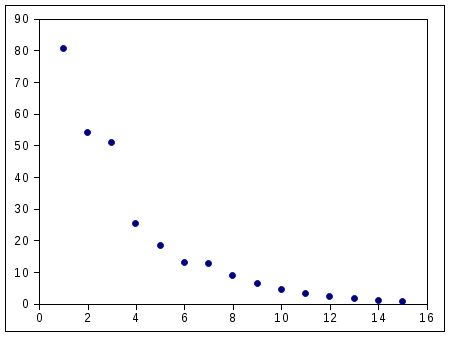
На рис. 6.2 показан график с исходными данными (круглые точки). Поскольку линейная регрессия для таких данных, очевидно, даёт плохие результаты, будем пытаться использовать нелинейные модели. Тогда этот процесс можно будет называть "non-linear fitting" – "нелинейная подгонка".
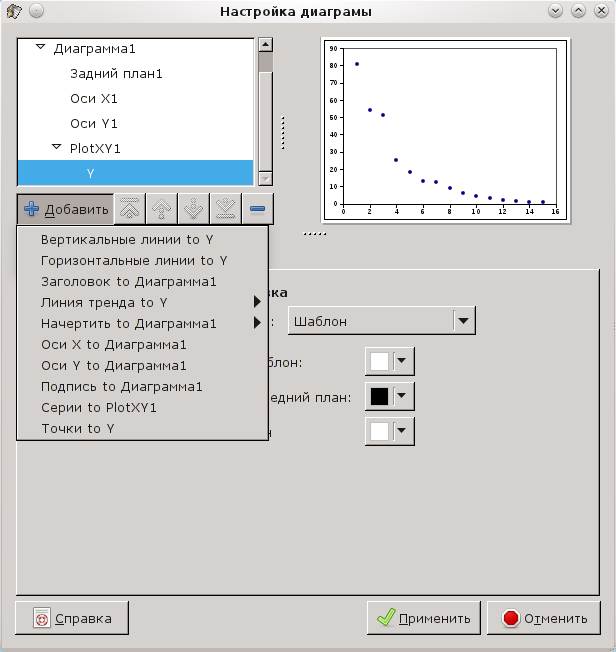
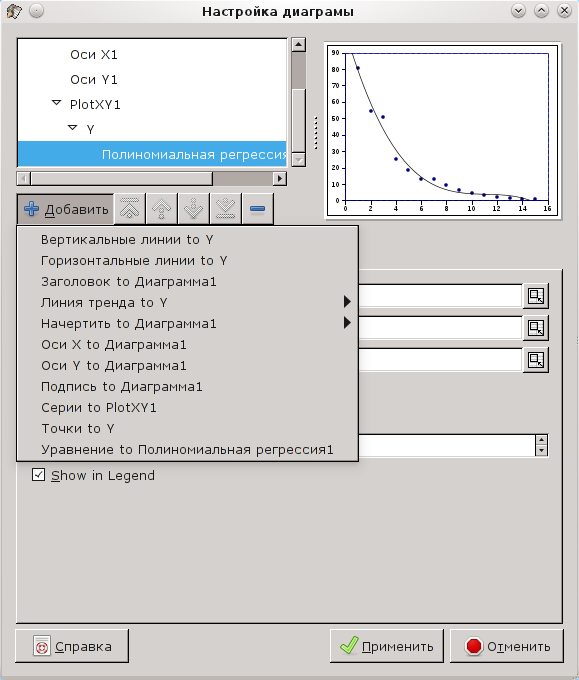
Для добавления кривых регрессии вызовем диалог настройки графика, выберем серию исходных данных ( ) и используем кнопку "Добавить" для выбора добавляемого объекта (рис. 6.3).
) и используем кнопку "Добавить" для выбора добавляемого объекта (рис. 6.3).
Во вложенном меню "Линия тренда to Y" имеется набор классов кривых (уравнений интерполяции, рис. 6.4).
Заметим, что в списке вариантов присутствуют "Экспоненциально сглаженная кривая" и "Скользящее среднее", которые рассматривались в главе про статистику.
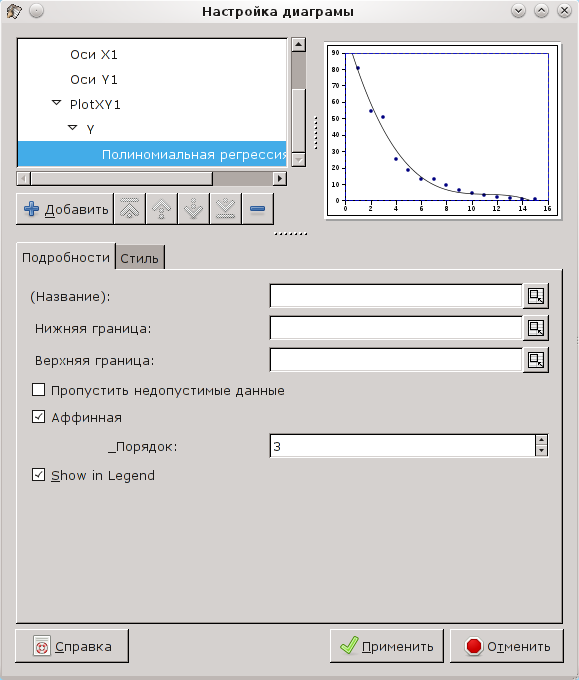
В качестве первой попытки описания экспериментальных данных выберем вариант интерполяции полиномом ("Полиномиальная"l) 3-го порядка (рис. 6.5).
Поле "Порядок" позволяет выбрать максимальную степень аргумента (порядок) в полиноме, а на вкладке "Стиль" можно настроить внешний вид линии.
Для того чтобы узнать коэффициенты полинома ещё раз нажмём кнопку "Добавить" и увидим, что в списке объектов появился объект "Уравнение to Полиномиальная регрессия1", как показано на рис. 6.6
Добавляемое на график уравнение кривой имеет собственный диалог настроек (рис. 6.7).
Режим "Показывать коэффициент регрессии  " ("Display regression coefficient
" ("Display regression coefficient  ") позволяет вывести под уравнением значение коэффициента парной корреляции, характеризующего "качество" интерполяции. Чем ближе это значение к 1, тем лучше подобрано уравнение регрессии.
") позволяет вывести под уравнением значение коэффициента парной корреляции, характеризующего "качество" интерполяции. Чем ближе это значение к 1, тем лучше подобрано уравнение регрессии.
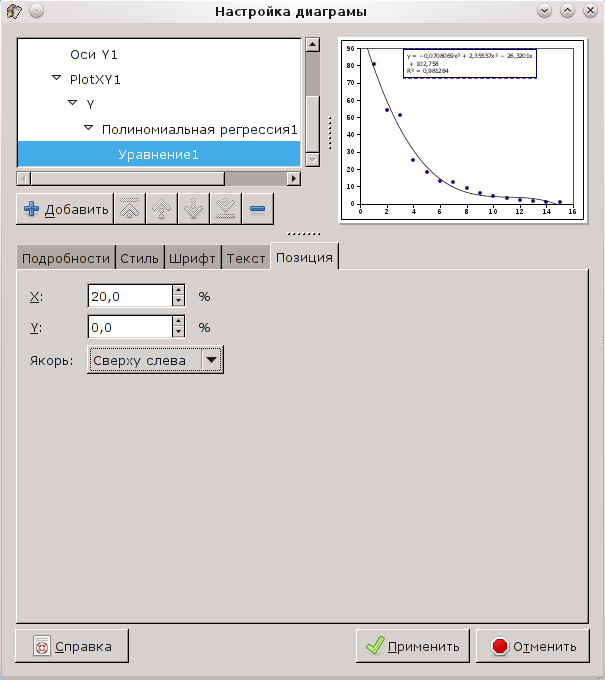
На вкладке "Позиция" можно задать желаемое место уравнения на графике в относительных единицах (рис. 6.8).
На вкладках "Стиль" и "Шрифт" задаётся стиль обрамления области с уравнением и шрифт для отображения уравнения.
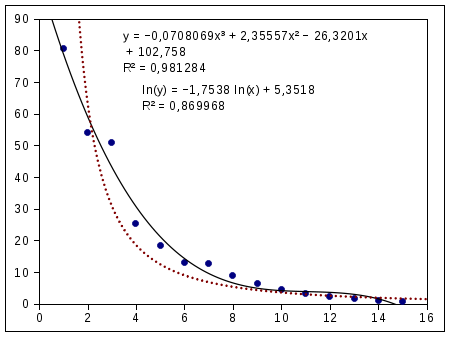
Для сравнения добавим интерполяцию степенной функцией ("Степенная"), установив стиль линии "точки" и толщину в 2 точки экрана (рис. 6.9). В этом случае модель имеет вид  , а на графике отображается линеаризованный вариант уравнения (через натуральный логарифм).
, а на графике отображается линеаризованный вариант уравнения (через натуральный логарифм).
Теперь можно пробовать другие варианты функций и следить за значением критерия  . Наилучшим описанием будет такое, при котором это значение, как уже упоминалось, будет максимально близко к 1.
. Наилучшим описанием будет такое, при котором это значение, как уже упоминалось, будет максимально близко к 1.
Вариант подгонки экспоненциальной зависимостью вида 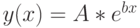 уже был показан в главе про статистику.
уже был показан в главе про статистику.
Таким образом, использование Gnumeric для подгонки экспериментальных данных даёт неплохие результаты для не очень сложных зависимостей и позволяет избежать использования громоздких и дорогостоящих математических пакетов программ.