НОУ ИНТУИТ | Проектирование систем искусственного интеллекта. Лекция 5: Методы и алгоритмы анализа структуры многомерных данных

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 15.06.2007 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 73 студентам

| Поделиться |

Поддержать программу

Кластерный анализ

Кластерный анализ предназначен для разбиения множества объектов на заданное или неизвестное число классов на основании некоторого математического критерия качества классификации (cluster (англ.) — гроздь, пучок, скопление, группа элементов, характеризуемых каким-либо общим свойством). Критерий качества кластеризации в той или иной мере отражает следующие неформальные требования:

внутри групп объекты должны быть тесно связаны между собой;
объекты разных групп должны быть далеки друг от друга;
при прочих равных условиях распределения объектов по группам должны быть равномерными.

Требования 1) и 2) выражают стандартную концепцию компактности классов разбиения; требование 3) состоит в том, чтобы критерий не навязывал объединения отдельных групп объектов.

Узловым моментом в кластерном анализе считается выбор метрики (или меры близости объектов), от которого решающим образом зависит окончательный вариант разбиения объектов на группы при заданном алгоритме разбиения. В каждой конкретной задаче этот выбор производится по-своему, с учетом главных целей исследования, физической и статистической природы используемой информации и т. п. При применении экстенсиональных методов распознавания, как было показано в предыдущих разделах, выбор метрики достигается с помощью специальных алгоритмов преобразования исходного пространства признаков.

Другой важной величиной в кластерном анализе является расстояние между целыми группами объектов. Приведем примеры наиболее распространенных расстояний и мер близости, характеризующих взаимное расположение отдельных групп объектов. Пусть w_i — i -я группа (класс, кластер) объектов, N_i — число объектов, образующих группу w_i, вектор 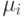$\mu_i$ — среднее арифметическое объектов, входящих в w_i (другими словами, 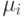$\mu_i$ — "центр тяжести" i-й группы), a q ( w_l, w_m ) — расстояние между группами w_l и w_m.

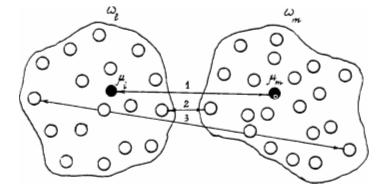
Различные способы определения расстояния между кластерами wl и wm: 1 — по центрам тяжести, 2 — по ближайшим объектам, 3 — по самым далеким объектам

Рис. 5.6. Различные способы определения расстояния между кластерами wl и wm: 1 — по центрам тяжести, 2 — по ближайшим объектам, 3 — по самым далеким объектам

Расстояние ближайшего соседа есть расстояние между ближайшими объектами кластеров:

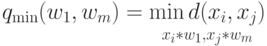
$q_{\min}(w_1,w_m)=\mathop{\min d(x_i,x_j)}\limits_{x_i*w_1, x_j*w_m}$

Расстояние дальнего соседа — расстояние между самыми дальними объектами кластеров:

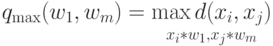
$q_{\max}(w_1,w_m)=\mathop{\max d(x_i,x_j)}\limits_{x_i*w_1, x_j*w_m}$

Расстояние центров тяжести равно расстоянию между центральными точками кластеров:

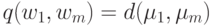
$q(w_1,w_m)=d(\mu_1,\mu_m)$

Обобщенное (по Колмогорову) расстояние между классами, или обобщенное K -расстояние, вычисляется по формуле $q_{\tau}^{(K)}(w_1,w_m)\left[\frac{1}{N_1 N_m} \sum\limits_{x_i*w_1} \sum\limits_{x_j*w_m} d^{\tau}(x_i,x_j)\right]^{\frac{1}{\tau}}$

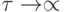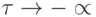В частности, при $\tau \to \propto$ и при $\tau \to -\propto$ имеем

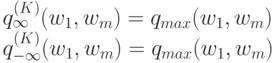
$q_{\infty}^{(K)}(w_1,w_m)=q_{max}(w_1,w_m)\\q_{-\infty}^{(K)}(w_1,w_m)=q_{max}(w_1,w_m)$

Выбор той или иной меры расстояния между кластерами влияет, главным образом, на вид выделяемых алгоритмами кластерного анализа геометрических группировок объектов в пространстве признаков. Так, алгоритмы, основанные на расстоянии ближайшего соседа, хорошо работают в случае группировок, имеющих сложную, в частности, цепочечную, структуру. Расстояние дальнего соседа применяется, когда искомые группировки образуют в пространстве признаков шаровидные облака. И промежуточное место занимают алгоритмы, использующие расстояния центров тяжести и средней связи, которые лучше всего работают в случае группировок эллипсоидной формы.

Нацеленность алгоритмов кластерного анализа на определенную структуру группировок объектов в пространстве признаков может приводить к неоптимальным или даже неправильным результатам, если гипотеза о типе группировок неверна. В случае отличия реальных распределений от гипотетических указанные алгоритмы часто "навязывают" данным не присущую им структуру и дезориентируют исследователя. Поэтому экспериментатор, учитывающий данный факт, в условиях априорной неопределенности прибегает к применению батареи алгоритмов кластерного анализа и отдает предпочтение какому-либо выводу на основании комплексной оценки совокупности результатов работы этих алгоритмов.

Алгоритмы кластерного анализа отличаются большим разнообразием. Это могут быть, например, алгоритмы, реализующие полный перебор сочетаний объектов или осуществляющие случайные разбиения множества объектов. В то же время большинство таких алгоритмов состоит из двух этапов. На первом этапе задается начальное (возможно, искусственное или даже произвольное) разбиение множества объектов на классы и определяется некоторый математический критерий качества автоматической классификации. Затем, на втором этапе, объекты переносятся из класса в класс до тех пор, пока значение критерия не перестанет улучшаться.

Многообразие алгоритмов кластерного анализа обусловлено также множеством различных критериев, выражающих те или иные аспекты качества автоматического группирования. Простейший критерий качества непосредственно базируется на величине расстояния между кластерами. Однако такой критерий не учитывает "населенность" кластеров — относительную плотность распределения объектов внутри выделяемых группировок. Поэтому другие критерии основываются на вычислении средних расстояний между объектами внутри кластеров. Но наиболее часто применяются критерии в виде отношений показателей "населенности" кластеров к расстоянию между ними. Это, например, может быть отношение суммы межклассовых расстояний к сумме внутриклассовых (между объектами) расстояний или отношение общей дисперсии данных к сумме внутриклассовых дисперсий и дисперсии центров кластеров.

Функционалы качества и конкретные алгоритмы автоматической классификации достаточно полно и подробно рассмотрены в специальной литературе. Эти функционалы и алгоритмы характеризуются различной трудоемкостью и подчас требуют ресурсов высокопроизводительных компьютеров. Разнообразные процедуры кластерного анализа входят в состав практически всех современных пакетов прикладных программ для статистической обработки многомерных данных.

Иерархическое группирование

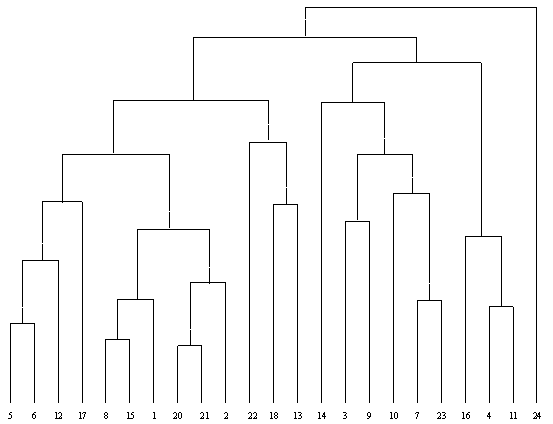
Рис. 5.7. Результаты работы иерархической агломеративной процедуры группирования объектов, представленные в виде дендрограммы

Классификационные процедуры иерархического типа предназначены для получения наглядного представления о стратификационной структуре всей исследуемой совокупности объектов. Эти процедуры основаны на последовательном объединении кластеров (агломеративные процедуры) и на последовательном разбиении (дивизимные процедуры). Наибольшее распространение получили агломеративные процедуры. Рассмотрим последовательность операций в таких процедурах.

На первом шаге все объекты считаются отдельными кластерами. Затем на каждом последующем шаге два ближайших кластера объединяются в один. Каждое объединение уменьшает число кластеров на один так, что в конце концов все объекты объединяются в один кластер. Наиболее подходящее разбиение выбирает чаще всего сам исследователь, которому предоставляется дендрограмма, отображающая результаты группирования объектов на всех шагах алгоритма (рис. 5.7). Могут одновременно также использоваться и математические критерии качества группирования.

Различные варианты определения расстояния между кластерами дают различные варианты иерархических агломеративных процедур. Учитывая специфику подобных процедур, для задания расстояния между классами оказывается достаточным указать порядок пересчета расстояний между классом w_l и классом w(m, n) являющимся объединением двух других классов w_m и w_n по расстояниям q_mт = q(w_m, w_n) и q_lт = q(w_l, w_n) между этими классами. В литературе предлагается следующая общая формула для вычисления расстояния между некоторым классом w_l и классом w(m, n):

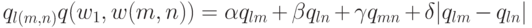
$q_{l(m,n)}q(w_1,w(m,n))=\alpha q_{lm}+\beta q_{ln} +\gamma q_{mn}+\delta |q_{lm}-q_{ln}|$

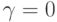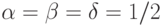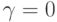где $\alpha ,\beta ,\gamma$ и $\delta$ — числовые коэффициенты, определяющие нацеленность агломеративной процедуры на решение той или иной экстремальной задачи. В частности, полагая $\alpha =\beta =-\delta =1/2$ и $\gamma =0$ , приходим к расстоянию, измеряемому по принципу ближайшего соседа. Если положить $\alpha =\beta =\delta =1/2$ и $\gamma =0$ , то расстояние между двумя классами определится как расстояние между двумя самыми далекими объектами этих классов, то есть это будет расстояние дальнего соседа. И, наконец, выбор коэффициентов соотношения по формулам

$\alpha =\frac{N_m}{N_m+N_n},\beta =\frac{N_n}{N_m+N_n},\gamma = \delta =0$

приводит к расстоянию q_cр между классами, вычисленному как среднее расстояние между всеми парами объектов, один из которых берется из одного класса, а другой из другого.

Использование следующей модификации формулы

$q^2_{l(m,n)}=\frac{N_1+N_m}{N_l+N_m+N_n}q^2_{lm} + \frac{N_l+N_n}{N_l+N_m+N_n}q^2_{ln} - \frac{N_l}{N_l+N_m+N_n}q^2_{mn}$

дает агломеративный алгоритм, приводящий к минимальному увеличению общей суммы квадратов расстояний между объектами внутри классов на каждом шаге объединения этих классов. В отличие от оптимизационных кластерных алгоритмов предоставляющих исследователю конечный результат группирования объектов, иерархические процедуры позволяют проследить процесс выделения группировок и иллюстрируют соподчиненность кластеров, образующихся на разных шагах какого-либо агломеративного или дивизимного алгоритма. Это стимулирует воображение исследователя и помогает ему привлекать для оценки структуры данных дополнительные формальные и неформальные представления.

Дальше >>

Проектирование систем искусственного интеллекта

Проектирование систем искусственного интеллекта

Методы и алгоритмы анализа структуры многомерных данных

Кластерный анализ

Иерархическое группирование

Вопросы и ответы

Студенты

Авторизоваться

Проектирование систем искусственного интеллекта

Проектирование систем искусственного интеллекта

Методы и алгоритмы анализа структуры многомерных данных

Кластерный анализ

Иерархическое группирование

Вопросы и ответы

Студенты