Адаптация и обучение

Адаптация — это процесс изменения параметров и структуры системы, а возможно, и управляющих воздействий, на основе текущей информации с целью достижения определенного состояния системы при начальной неопределенности и изменяющихся условиях работы.

Обучение — это процесс, в результате которого система постепенно приобретает способность отвечать нужными реакциями на определенные совокупности внешних воздействий, а адаптация — это подстройка параметров и структуры системы с целью достижения требуемого качества управления в условиях непрерывных изменений внешних условий.

Персептроны

Пока о проблеме обучения распознаванию образов удавалось говорить в общих чертах, не выделяя конкретные методы или алгоритмы, — не возникало и трудностей, появляющихся всяких раз, когда приходится иметь дело с огромным множеством примеров, у которых общий подход к решению проблемы ОРО. Коварство самой проблемы состоит в том, что, на первый взгляд, все методы и алгоритмы кажутся совершенно различными и, что самое неприятное, часто никакой из них не годится для решения той задачи, которую крайне необходимо срочно решить. И тогда появляется желание выдумать новый алгоритм, который, может быть, достигнет цели. Очевидно, именно это привело к возникновению огромного множества алгоритмов, в котором не так-то легко разобраться.

Один из методов решения задач обучения распознаванию образов основан на моделировании гипотетического механизма человеческого мозга. Структура модели заранее постулируется. При таком подходе уровень биологических знаний или гипотез о биологических механизмах является исходной предпосылкой, на которой базируются модели этих механизмов. Примером такого направления в теории и практике проблемы ОРО является класс устройств, называемых персептронами. Нужно отметить, что персептроны на заре своего возникновения рассматривались только как эвристические модели механизма мозга. Впоследствии они стали основополагающей схемой в построении кусочно-линейных моделей, обучающихся распознаванию образов.

Рис. 4.1. Персептрон

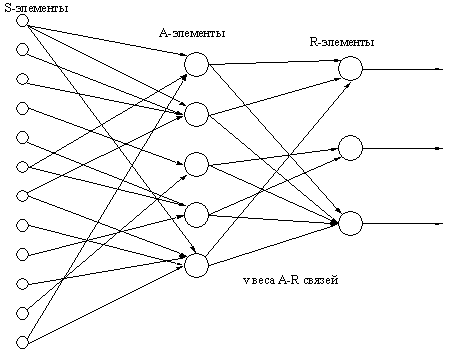
В наиболее простом виде персептрон (рис. 4.1.) состоит из совокупности чувствительных (сенсорных) элементов ( S -элементов), на которые поступают входные сигналы. S -элементы случайным образом связаны с совокупностью ассоциативных элементов ( А -элементов), выход которых отличается от нуля только тогда, когда возбуждено достаточно большое число S-элементов, воздействующих на один А -элемент. А -элементы соединены с реагирующими элементами ( R -элементами) связями, коэффициенты усиления ( v ) которых переменны и изменяются в процессе обучения. Взвешенные комбинации выходов R -элементов составляют реакцию системы, которая указывает на принадлежность распознаваемого объекта определенному образу. Если распознаются только два образа, то в персептроне устанавливается только один R -элемент, который обладает двумя реакциями — положительной и отрицательной. Если образов больше двух, то для каждого образа устанавливают свой R -элемент, а выход каждого такого элемента представляет линейную комбинацию выходов A -элементов:

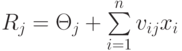( 4.1)

где R_j — реакция j -го R -элемента; x_i — реакция i -го A -элемента; v_ij — вес связи от i -го A -элемента к j -му R элементу; 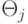— порог j -го R -элемента.

Аналогично записывается уравнение i -го A -элемента:

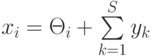( 4.2)

Здесь сигнал y_k может быть непрерывным, но чаще всего он принимает только два значения: 0 или 1. Сигналы от S -элементов подаются на входы А -элементов с постоянными весами, равными единице, но каждый А -элемент связан только с группой случайно выбранных S -элементов. Предположим, что требуется обучить персептрон различать два образа V₁ и V₂. Будем считать, что в персептроне существует два R -элемента, один из которых предназначен образу V₁, а другой — образу V₂. Персептрон будет обучен правильно, если выход R₁ превышает R₂, когда распознаваемый объект принадлежит образу V₁, и наоборот. Разделение объектов на два образа можно провести и с помощью только одного R -элемента. Тогда объекту образа V₁ должна соответствовать положительная реакция R -элемента, а объектам образа V₂ — отрицательная.

Персептрон обучается путем предъявления обучающей последовательности изображений объектов, принадлежащих образам V₁ и V₂. В процессе обучения изменяются веса v_i А -элементов. В частности, если применяется система подкрепления с коррекцией ошибок, прежде всего учитывается правильность решения, принимаемого персептроном. Если решение правильно, то веса связей всех сработавших А -элементов, которые ведут к R -элементу, выдавшему правильное решение, увеличиваются, а веса несработавших А -элементов остаются неизменными. Можно оставлять неизменными веса сработавших А -элементов, но уменьшать веса несработавших. В некоторых случаях веса сработавших связей увеличивают, а несработавших — уменьшают. После процесса обучения персептрон сам, без учителя, начинает классифицировать новые объекты.

Если персептрон действует по описанной схеме и в нем допускаются лишь связи, идущие от бинарных S -элементов к A -элементам и от A -элементов к единственному R -элементу, то такой персептрон принято называть элементарным -персептроном. Обычно классификация C(W) задается учителем. Персептрон должен выработать в процессе обучения классификацию, задуманную учителем.

О персептронах было сформулировано и доказано несколько основополагающих теорем, две из которых, определяющие основные свойства персептрона, приведены ниже.

Теорема 1. Класс элементарных -персептронов, для которых существует решение для любой задуманной классификации, не является пустым.

Эта теорема утверждает, что для любой классификации обучающей последовательности можно подобрать такой набор (из бесконечного набора) А -элементов, в котором будет осуществлено задуманное разделение обучающей последовательности при помощи линейного решающего правила .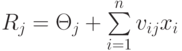

Теорема 2. Если для некоторой классификации C(W) решение существует, то в процессе обучения -персептрона с коррекцией ошибок, начинающегося с произвольного исходного состояния, это решение будет достигнуто в течение конечного промежутка времени.

Смысл этой теоремы состоит в том, что если относительно задуманной классификации можно найти набор А-элементов, в котором существует решение, то в рамках этого набора оно будет достигнуто в конечный промежуток времени.

Обычно обсуждают свойства бесконечного персептрона, т. е. персептрона с бесконечным числом А-элементов со всевозможными связями с S -элементами (полный набор A -элементов). Для таких персептронов решение всегда существует, а раз оно существует, то оно и достижимо в -персептронах с коррекцией ошибок.

Очень интересную область исследований представляют собой многослойные персептроны и персептроны с перекрестными связями, но теория этих систем практически еще не разработана.