|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Алгоритмы нечеткой оптимизации
Нечеткие цели, ограничения и решения
Непрерывно возрастающая сложность технологии контролируемых объектов настоятельно нуждалась в централизованном управлении и поэтому вызвала к жизни иерархическую структуру принятия решений. Поэтому появилась необходимость разделения всего процесса принятия решений управления на такое число уровней, чтобы решение задачи оптимизации на каждом из них было не сложным. Но с возникновением многоуровневых иерархических систем управления появилась и новая задача согласования и координации решений, принимаемых на всех уровнях.
Общая схема координации в двухуровневой системе сводится к следующему. Элементы передают в центр набор вариантов своей работы. Каждый вариант представляет собой векторный показатель элемента, допустимый с точки зрения его локальных ограничений. На основании получаемых вариантов центр формирует план, оптимальный с точки зрения всей системы. Этот план передается элементам и далее детализируется ими.
Однако при моделировании сложных систем невозможно учесть достаточно большое число реальных факторов, поскольку это привело бы к чрезмерному усложнению модели. Поэтому в модель приходится вводить лишь ограниченное число таких факторов, которые по тем или иным соображениям считаются наиболее существенными. При этом возможны два подхода. Неучтенные в описании модели факторы можно считать абсолютно несущественными и полностью их игнорировать при принятии решений с использованием этой модели. С другой стороны, при втором подходе можно явно не вводить "несущественные факторы" в математическую модель, но учитывать их влияние, допуская, что отклик модели на то или иное воздействие (выбор альтернативы) может быть известен лишь приближенно или нечетко.
В традиционном подходе главными элементами процесса принятия решения являются:
- Множество альтернатив.
- Множество ограничений, которые необходимо учитывать при выборе между различными альтернативами.
- Функция предпочтительности, определяющая переход из пространства альтернатив в некоторое другое пространство и ставящая каждой альтернативе в соответствие выигрыш (или проигрыш), который получают в результате выбора этой альтернативы.
При рассмотрении этого процесса с более общих позиций принятия решений в нечетких условиях естественной представляется другая логическая схема, отличительной чертой которой является симметрия по отношению к целям и ограничениям. Этот подход устраняет различия между целями и ограничениями и позволяет достаточно просто принять на их основе решение.
Под нечеткой целью подразумевается цель, которую можно описать как
нечеткое
множество в соответствующем пространстве. Пусть  —
заданное множество
альтернатив. Тогда нечеткая цель, или просто цель,
—
заданное множество
альтернатив. Тогда нечеткая цель, или просто цель,  будет
определяться
фиксированным нечетким множеством
будет
определяться
фиксированным нечетким множеством  в
в  .
.
При обычном подходе функция предпочтительности, используемая в процессе
принятия
решения, служит для установления линейной упорядоченности на множестве
альтернатив.
Очевидно, что функция принадлежности 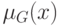 нечеткой цели выполняет
ту же задачу и может быть получена из функции предпочтительности с помощью
нормализации, сохраняющей установленную линейную упорядоченность.
нечеткой цели выполняет
ту же задачу и может быть получена из функции предпочтительности с помощью
нормализации, сохраняющей установленную линейную упорядоченность.
Подобным же образом нечеткое ограничение  в пространстве
в пространстве  определяется как некоторое нечеткое множество в
определяется как некоторое нечеткое множество в  . Важным
моментом здесь
является то, что и нечеткая цель, и нечеткое ограничение рассматриваются
как нечеткие множества в пространстве альтернатив; это дает возможность
не делать между ними различия при формировании решения.
. Важным
моментом здесь
является то, что и нечеткая цель, и нечеткое ограничение рассматриваются
как нечеткие множества в пространстве альтернатив; это дает возможность
не делать между ними различия при формировании решения.
Решение — это
по существу выбор одной или нескольких из имеющихся альтернатив.
Проблема принятия решения в нечетких условиях интерпретируется тогда
как комплексное влияние нечеткой цели  и нечеткого ограничения
и нечеткого ограничения  на выбор альтернатив и характеризуется пересечением
на выбор альтернатив и характеризуется пересечением  ,
которое и образует
нечеткое множество решений
,
которое и образует
нечеткое множество решений  , т.е.
, т.е.
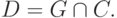
Функция принадлежности для множества решений задается соотношением

В общем случае, если имеется  нечетких целей и
нечетких целей и  нечетких
ограничений, то результирующее решение определяется пересечением всех
заданных целей и ограничений, т.е.
нечетких
ограничений, то результирующее решение определяется пересечением всех
заданных целей и ограничений, т.е.

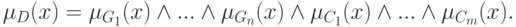
В приведенном определении нечеткие цели и нечеткие ограничения
входят в выражение  совершенно одинаковым образом. Такое
определение
решения как нечеткого множества в пространстве альтернатив может
показаться несколько искусственным. На самом деле оно совершенно естественно,
поскольку нечеткое решение может рассматриваться как некоторая
"инструкция",
неформальность которой является следствием неточности формулировки
поставленных целей и ограничений.
совершенно одинаковым образом. Такое
определение
решения как нечеткого множества в пространстве альтернатив может
показаться несколько искусственным. На самом деле оно совершенно естественно,
поскольку нечеткое решение может рассматриваться как некоторая
"инструкция",
неформальность которой является следствием неточности формулировки
поставленных целей и ограничений.
Во многих случаях все же разумно выбирать те альтернативы, которые имеют
максимальную степень принадлежности к  . Если таких элементов
несколько,
то они образуют обычное множество, которое называется оптимальным
решением, а каждый элемент этого множества — максимизирующим
решением.
. Если таких элементов
несколько,
то они образуют обычное множество, которое называется оптимальным
решением, а каждый элемент этого множества — максимизирующим
решением.
Для практики интересен более общий случай, когда нечеткие цели и нечеткие ограничения — нечеткие множества в разных пространствах.
Пусть  — отображение из
— отображение из  в
в  , причем переменная
, причем переменная  обозначает входное
воздействие, а
обозначает входное
воздействие, а  — соответствующий выход.
— соответствующий выход.
Предположим, что нечеткая цель задана как нечеткое множество  в
в  , в то время
как нечеткое
ограничение — нечеткое множество
, в то время
как нечеткое
ограничение — нечеткое множество  в пространстве
в пространстве  .
Имея нечеткое множество
.
Имея нечеткое множество  в
в  , можно найти нечеткое
множество
, можно найти нечеткое
множество  в
в  ,
которое индуцирует
,
которое индуцирует  в
в  . Функция принадлежности
. Функция принадлежности  в
в  задается равенством
задается равенством
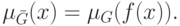
После этого решение  может быть выражено пересечением
множеств
может быть выражено пересечением
множеств  и
и  .
Используя предыдущее соотношение, можно записать
.
Используя предыдущее соотношение, можно записать
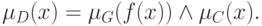
Таким образом, случай, когда нечеткие цели и нечеткие ограничения задаются как нечеткие множества в разных пространствах, может быть сведен к случаю, когда они задаются в одном и том же пространстве.
