|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Алгоритмы нечеткой оптимизации
Модели нечеткой ожидаемой полезности
При описании индивидуального принятия решения в рамках классического подхода, наряду с моделями математического программирования, широко применяются теория статистических решений и теория ожидаемой полезности. Последняя предназначена для анализа решений, когда неопределенность обусловлена отсутствием объективной физической шкалы для оценки предпочтительности альтернатив. В этих случаях используется субъективная шкала полезности лица, принимающего решение (ЛПР). В реальных ситуациях исходы, соответствующие принятым решениям (состояниям системы), являются подчас неточными, что влечет за собой размытость соответствующих им оценок функции полезности. Размытый вариант ожидаемой полезности формулируется, например, в модели, где выделяются и одновременно учитываются как случайные, так и нечеткие составляющие неопределенности. Выбор происходит на основе максимизации нечеткой ожидаемой полезности
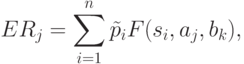
 — размытая вероятность состояния
— размытая вероятность состояния 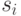 из множества
состояний мира
из множества
состояний мира  ,
, 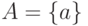 — множество альтернатив,
— множество альтернатив,  — множество критериев,
— множество критериев,  —
множество оценок, а
—
множество оценок, а ![\(\wp (R) = \{ \mu _R \;|\;\mu _R :\;R \to [0,1]\}\)](/sites/default/files/tex_cache/5f177e097732b49e24bd94e3b39c8c99.png) —
класс всех нечетких подмножеств на множестве оценок
—
класс всех нечетких подмножеств на множестве оценок  .
.Существуют модели, в которых описываются нечеткие лотереи, нечеткие деревья предпочтения, нечеткие байесовские оценки и т.п., где неполнота информации о законе распределения вероятности моделируется с использованием нечетких чисел и лингвистических вероятностей.
Например, задача анализа решений формулируется следующим образом.
Пусть имеются две обычные вероятности лотереи: ![A = \left[ {pu_{A_1 } ,\;(1 - p)u_{A_2 } } \right]](/sites/default/files/tex_cache/938e752740f3015346605e230bea4e5c.png) , где
, где  —
вероятность исхода с ожидаемой полезностью
—
вероятность исхода с ожидаемой полезностью 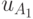 и
и  —
вероятность исхода с ожидаемой полезностью
—
вероятность исхода с ожидаемой полезностью 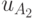 ,
а
,
а ![\(B = \left[ {qu_{B_1 } ,\;(1 - q)u_{B_2 } } \right]\)](/sites/default/files/tex_cache/b0053d3081073393e33177317fc1511a.png) , где
, где  —
вероятность исхода с ожидаемой полезностью
—
вероятность исхода с ожидаемой полезностью 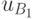 ,
,  —
вероятность исхода с ожидаемой полезностью
—
вероятность исхода с ожидаемой полезностью 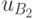 . Из теории
ожидаемой полезности следует, что
. Из теории
ожидаемой полезности следует, что  , если
, если

Будем считать, что вероятности  и
и  и ожидаемые
полезности
и ожидаемые
полезности 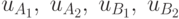 точно
не известны, т.е. введем
точно
не известны, т.е. введем
![\mu _P :\;P \to [0,1],\quad \mu _Q :\;Q \to [0,1],\quad \mu
_U :\;U \to [0,1].](/sites/default/files/tex_cache/8d04aab1b3a3aed4286d1da1880d53ae.png)
Тогда, в соответствии с принципом обобщения, степени принадлежности
альтернатив  и
и  множествам нечетких ожидаемых
полезностей в нечетких
лотереях
множествам нечетких ожидаемых
полезностей в нечетких
лотереях  и
и  соответственно вычисляются
соответственно вычисляются
![\begin{gathered}
\mu _A (a) = \mathop {\max }\limits_{pu_{A1} + (1 - p)u_{A2} = a} \;\left[
{\min \{ \mu _P (p),\;\mu _{A_1 } (u_{A_1 } ),\;\mu _{A_2 } (u_{A_2 } )\} }
\right], \\
\mu _B (b) = \mathop {\max }\limits_{qu_{B1} + (1 - q)u_{B2} = b} \;\left[
{\min \{ \mu _P (p),\;\mu _{B_1 } (u_{B_1 } ),\;\mu _{B_2 } (u_{B_2 } )\} }
\right]. \\
\end{gathered}](/sites/default/files/tex_cache/032866a4b87058e8bb5cc5fbd37e9109.png)
В случае лотереи с  исходами также для каждого ребра дерева
решений подсчитывается значение нечеткой ожидаемой полезности.
исходами также для каждого ребра дерева
решений подсчитывается значение нечеткой ожидаемой полезности.
