|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Нечеткие алгоритмы обучения
Известно, что обучающиеся системы улучшают функционирование в процессе работы, модифицируя свою структуру или значение параметров. Предложено большое число способов описания и построения обучающихся систем. Все они предполагают решение следующих задач: выбор измерений (свойств, рецепторов); поиск отображения пространства рецепторов в пространство признаков, которые осуществляют вырожденное отображение объектов; поиск критерия отбора признаков. Причем в различных задачах для получения хороших признаков могут понадобиться разные критерии отбора. При обучении необходимо отвлечься от различий внутри класса, сосредоточить внимание на отличии одного класса от другого и на сходстве внутри классов. Необходим достаточный уровень начальной организации обучающейся системы. Для сложной структурной информации необходима многоуровневая обучающаяся система.
Следует выделить следующие группы нечетких алгоритмов обучения: обучающийся нечеткий автомат, обучение на основе условной нечеткой меры, адаптивный нечеткий логический регулятор, обучение при лингвистическом описании предпочтения.
Рекуррентные соотношения в алгоритмах первых двух групп позволяют получать функцию принадлежности исследуемого понятия на множестве заранее известных элементов. В третьей группе нечеткий алгоритм обучения осуществляет модификацию нечетких логических правил для удержания управляемого процесса в допустимых границах. В четвертой группе нечеткий алгоритм обучения осуществляет поиск вырожденного отображения пространства свойств в пространство полезных признаков и модификацию на их основе описания предпочтения.
Обучающийся нечеткий автомат
Рассмотрим автомат с четким входом 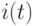 и зависимым от времени
нечетким
отношением перехода
и зависимым от времени
нечетким
отношением перехода 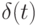 . Пусть
. Пусть 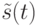 —
нечеткое состояние
автомата в момент времени
—
нечеткое состояние
автомата в момент времени  на конечном множестве состояний
на конечном множестве состояний 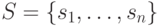 и
и 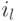 — оценка значения
— оценка значения 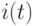 .Состояние
автомата в момент времени
.Состояние
автомата в момент времени 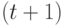 определяется
определяется  -
- 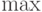 композицией:
композицией:


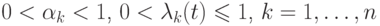 .
Константа
.
Константа 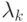 определяет скорость обучения. Начало
работы автомата
возможно без априорной информации
определяет скорость обучения. Начало
работы автомата
возможно без априорной информации  или 1, а
также с априорной
информацией
или 1, а
также с априорной
информацией 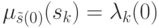 . Величина
. Величина 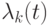 зависит от оценки функционирования автомата. Доказано, что имеет место
сходимость матрицы переходов, независимо от того, есть ли априорная информация,
т.е.
зависит от оценки функционирования автомата. Доказано, что имеет место
сходимость матрицы переходов, независимо от того, есть ли априорная информация,
т.е.  может быть любым значением из интервала
может быть любым значением из интервала ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.Пример.
На рис. 12.1 изображена модель классификации образов. Роль входа и выхода
можно кратко объяснить следующим образом. Во время каждого интервала
времени классификатор образов получает новый образец 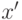 из неизвестной
внешней среды. Далее
из неизвестной
внешней среды. Далее 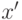 обрабатывается в рецепторе, из которого поступает
как в блок "обучаемый", так и в блок "учитель" для
оценки.
Критерий оценки должен быть выбран так, чтобы его минимизация или максимизация
отражала свойства классификации (классов образов). Поэтому, благодаря
естественному распределению образов, критерий может быть включен в систему,
чтобы служить в качестве учителя для классификатора. Модель обучения
формируется
следующим образом. Предполагается, что классификатор имеет в распоряжении
множество дискриминантных функций нескольких переменных. Система адаптируется
к лучшему
решению. Лучшее решение выделяет множество дискриминантных функций, которые
дают
минимум нераспознавания среди множества дискриминантных функций для данного
множества
образцов.
обрабатывается в рецепторе, из которого поступает
как в блок "обучаемый", так и в блок "учитель" для
оценки.
Критерий оценки должен быть выбран так, чтобы его минимизация или максимизация
отражала свойства классификации (классов образов). Поэтому, благодаря
естественному распределению образов, критерий может быть включен в систему,
чтобы служить в качестве учителя для классификатора. Модель обучения
формируется
следующим образом. Предполагается, что классификатор имеет в распоряжении
множество дискриминантных функций нескольких переменных. Система адаптируется
к лучшему
решению. Лучшее решение выделяет множество дискриминантных функций, которые
дают
минимум нераспознавания среди множества дискриминантных функций для данного
множества
образцов.


