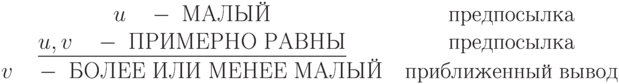Теория приближенных рассуждений

Под приближенными рассуждениями понимается процесс, при котором из нечетких посылок получают некоторые следствия, возможно, тоже нечеткие. Приближенные рассуждения лежат в основе способности человека понимать естественный язык, разбирать почерк, играть в игры, требующие умственных усилий, в общем, принимать решения в сложной и не полностью определенной среде. Эта способность рассуждений в качественных, неточных терминах отличает интеллект человека от интеллекта вычислительной машины.

Основным правилом вывода в традиционной логике является правило modus ponens, согласно которому мы судим об истинности высказывания по истинности высказываний и 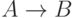. Например, если — высказывание "Джон в больнице", — высказывание "Джон болен", то если истинны высказывания "Джон в больнице" и "Если Джон в больнице, то он болен", то истинно и высказывание "Джон болен".

Во многих привычных рассуждениях, однако, правило modus ponens используется не в точной, а в приближенной форме. Так, обычно мы знаем, что истинно и что 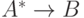, где 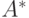есть, в некотором смысле, приближение . Тогда из 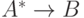мы можем сделать вывод о том, что приближенно истинно.

Далее мы обсудим способ формализации приближенных рассуждений, основанный на понятиях, введенных нами на предыдущей лекции. Однако, в отличие от традиционной логики, нашим главным инструментом будет не правило modus ponens, а так называемое композиционное правило вывода, весьма частным случаем которого является правило modus ponens.

Композиционное правило вывода

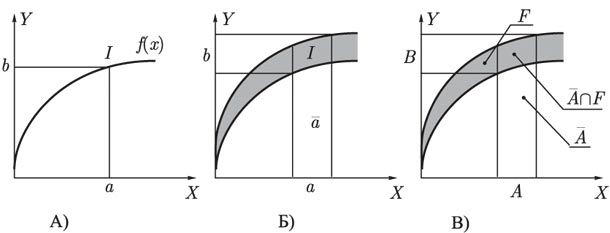
Композиционное правило вывода — это всего лишь обобщение следующей знакомой процедуры. Предположим, что имеется кривая 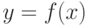(см. рис. 10.1(А)) и задано значение 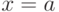. Тогда из того, что 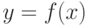и 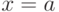, мы можем заключить, что .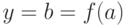

Обобщим теперь этот процесс, предположив, что — интервал, а — функция, значения которой суть интервалы, как на рисунке 10.1(Б). В этом случае, чтобы найти интервал , соответствующий интервалу , мы сначала построим цилиндрическое множество 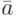с основанием и найдем его пересечение с кривой, значения которой суть интервалы. Затем спроектируем это пересечение на ось 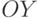и получим желаемое значение в виде интервала .

Рис. 10.1.

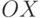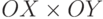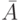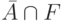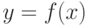Чтобы продвинуться еще на один шаг по пути обобщения, предположим, что — нечеткое подмножество оси , а — нечеткое отношение в (см. рис. 10.1(В)). Вновь образуя цилиндрическое нечеткое множество с основанием и его пересечение с нечетким отношением , мы получим нечеткое множество , которое является аналогом точки пересечения I на рис. 10.1(А). Таким образом, из того, что и 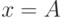— нечеткое подмножество оси 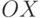, мы получаем значение в виде нечеткого подмножества оси .

Правило. Пусть и — два универсальных множества с базовыми переменными и , соответственно. Пусть и — нечеткие подмножества множеств и . Тогда композиционное правило вывода утверждает, что из нечетких множеств и следует нечеткое множество . Согласно определению композиции нечетких множеств, получим

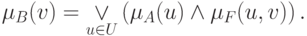
Пример. Пусть ,

A = МАЛЫЙ ,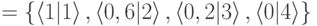

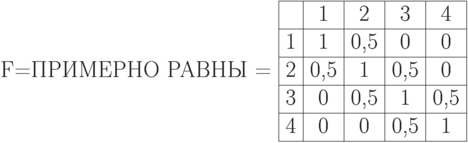
Тогда получим

B = БОЛЕЕ ИЛИ МЕНЕЕ МАЛЫЙ,

если терм БОЛЕЕ ИЛИ МЕНЕЕ определяется как оператор увеличения нечеткости.

Словами этот приближенный вывод можно записать в виде