|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Классы нечетких отношений
Задачи нечеткого упорядочения
Любую задачу принятия решений можно сформулировать как задачу отыскания
максимального элемента в множестве альтернатив с заданным в нем отношением
предпочтения. Однако во многих реальных ситуациях в множестве альтернатив
можно определить лишь нечеткое отношение предпочтения, т.е. указать для
каждой пары альтернатив  и
и  лишь степени, с
которыми выполняются
предпочтения
лишь степени, с
которыми выполняются
предпочтения  и
и  . В таких случаях задача
принятия решения становится неопределенной, поскольку неясно, что такое
максимальный элемент для нечеткого отношения предпочтения. Для двух типов нечетких отношений
можно предложить способы упорядочения элементов конечного множества, в котором
задано нечеткое отношение. Способы эти сводятся к тому, что для каждого из
рассматриваемых типов нечетких отношений строится некоторая функция (напоминающая функцию
полезности), и элементы множества упорядочиваются по соответствующим им
значениям этой функции.
. В таких случаях задача
принятия решения становится неопределенной, поскольку неясно, что такое
максимальный элемент для нечеткого отношения предпочтения. Для двух типов нечетких отношений
можно предложить способы упорядочения элементов конечного множества, в котором
задано нечеткое отношение. Способы эти сводятся к тому, что для каждого из
рассматриваемых типов нечетких отношений строится некоторая функция (напоминающая функцию
полезности), и элементы множества упорядочиваются по соответствующим им
значениям этой функции.
Пусть 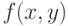 — функция принадлежности бинарного нечеткого
отношения в множестве
— функция принадлежности бинарного нечеткого
отношения в множестве  (например, отношения нестрого
предпочтения).
Допустим, что рассматривается задача упорядочения элементов конечного
множества
(например, отношения нестрого
предпочтения).
Допустим, что рассматривается задача упорядочения элементов конечного
множества  . Упорядочение можно
осуществлять по значениям следующей функции:
. Упорядочение можно
осуществлять по значениям следующей функции:

 , а функция
, а функция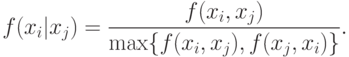
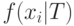 удобно пользоваться
следующим равенством:
удобно пользоваться
следующим равенством: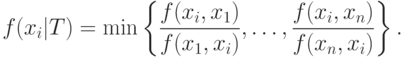
 является элемент
является элемент  такой, что
такой, что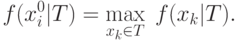
Рассмотрим еще одну задачу упорядочения, иллюстрируемую следующим примером.
Требуется решить, кто из детей: старший сын  , младший сын
, младший сын  или дочь
или дочь 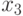 больше всего похож на отца
больше всего похож на отца  . Заданы "результаты
измерений":
. Заданы "результаты
измерений":  и
и  взятые отдельно, похожи на отца со степенями
взятые отдельно, похожи на отца со степенями  и
и  соответственно;
соответственно;  и
и 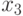 ,
взятые отдельно, похожи на отца со степенями
,
взятые отдельно, похожи на отца со степенями  и
и 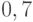 ; наконец,
; наконец,  и
и 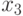 ,
взятые отдельно, похожи на отца со степенями
,
взятые отдельно, похожи на отца со степенями  и
и 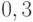 .
.
Таким образом, в этой задаче, в отличие от предыдущей, имеется стандартный
элемент (шаблон) для упорядочиваемого множества  , т.е. элемент,
обладающий
свойствами, общими для всех элементов этого множества. Иначе говоря, если
, т.е. элемент,
обладающий
свойствами, общими для всех элементов этого множества. Иначе говоря, если 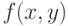 —
нечеткое отношение в
—
нечеткое отношение в  (например, отношение сходства), то
(например, отношение сходства), то

При наличии стандартного элемента для каждой пары элементов  и
и  множества
множества  задаются величины
задаются величины  ,
, 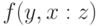 , т.е.
степени отношения (например, сходства)
, т.е.
степени отношения (например, сходства)  и
и  , взятых отдельно, к
, взятых отдельно, к  .
Упорядочение элементов множества
.
Упорядочение элементов множества  с заданным
таким способом нечетким отношением предлагается осуществлять в соответствии
со значениями функции
с заданным
таким способом нечетким отношением предлагается осуществлять в соответствии
со значениями функции
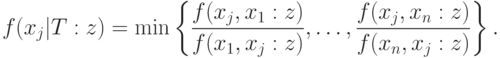
Максимальным в смысле этого упорядочения является элемент  такой,
что
такой,
что

Для задачи о сходстве отца и детей значения этой функции таковы:
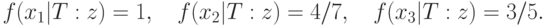
Отсюда вытекает, что наиболее похож на отца старший сын, затем следуют дочь и младший сын.

