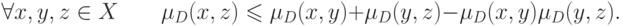Классы нечетких отношений

Отношения сходства и различия

Симметричное и рефлексивное нечеткое отношение сходства является аналогом обычного отношения толерантности. Нечеткие отношения сходства обычно задаются с помощью матриц сходства, связи между объектами, либо с помощью неориентированных взвешенных графов. Матрицы сходства могут быть получены как в результате измерения некоторого физического параметра, так и в результате опроса экспертов, которые для каждой пары объектов из указывают их степень сходства в некоторой шкале сравнений.

Условие транзитивности для нечетких отношений сходства обычно формулируются в виде

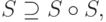
• ( )-транзитивность
  
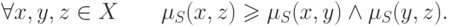
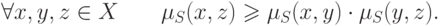
• ( )-транзитивность
  
• ( )-транзитивность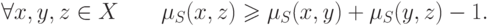
  

Наиболее интересными свойствами обладает ( )-транзитивное отношение сходства , которое является обобщением обычного отношения эквивалентности. Это отношение называется нечетким отношением эквивалентности или отношением подобия. Нетрудно показать, что любой -уровень нечеткого отношения эквивалентности является обычным отношением эквивалентности и, следовательно, определяет разбиение множества объектов на непересекающиеся классы эквивалентности. Из вложенности -уровней нечеткого отношения следует и вложенность разбиений множества , соответствующих различным -уровням, причем с уменьшением происходит укрупнение классов эквивалентности -уровней. Таким образом, нечеткое отношение эквивалентности задает иерархическую совокупность разбиений множества на непересекающиеся классы эквивалентности.

Нечеткое отношение эквивалентности, в отличие от произвольного отношения сходства, определяет совокупность разбиений множества на классы эквивалентности, благодаря тому, что условие транзитивности накладывает дополнительно сильные ограничения на возможные значения степени принадлежности. В случае, когда , отношение сходства транзитивно тогда и только тогда, если для любых из трех чисел 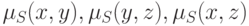, по крайней мере, два числа равны друг другу и по величине не превышают третье. Таким образом, нечеткое отношение эквивалентности обладает многими полезными свойствами из-за своего довольно специфического вида.

отношением различия называется симметричное и антирефлексивное нечеткое отношение. Отношение различия двойственно отношению сходства. В случае, когда , эти отношения могут быть получены друг из друга с помощью соотношения:

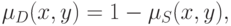
Ультраметрикой называется отношение различия, удовлетворяющее следующему неравенству:

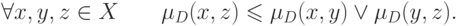
Очевидно, что это условие двойственно условию ( )-транзитивности. Понятие ультраметрики первоначально возникло и изучалось в кластерном анализе при исследовании свойств меры различия между объектами, определяющих естественное представление множества объектов в виде дерева разбиений. Представление ультраметрики с помощью системы вложенных друг в друга отношений эквивалентности было также известно в кластерном анализе, однако лишь в рамках теории нечетких отношений это представление получило естественное объяснение.

Метрикой называется отношение различия, удовлетворяющее неравенству треугольника:

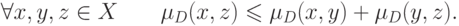
От метрики обычно требуют выполнения условия сильной антирефлексивности. Метрика, удовлетворяющая лишь простому условию антирефлексивности, называется псевдометрикой. Двойственным по отношению к метрике является ( )-транзитивное отношение сходства.

Двойственным условию ( )-транзитивности является следующее условие: