НОУ ИНТУИТ | Микроэкономика фирмы. Лекция 4: Поведение фирмы на товарных рынках

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 10.08.2007 | Уровень: для всех | Доступ: платный | ВУЗ: Национальный исследовательский университет "Высшая Школа Экономики"

|

Вам нравится? Нравится 35 студентам

| Поделиться |

Поддержать программу

2. Индекс Херфиндаля-Хиршмана

Индекс Херфиндаля-Хиршмана определяется как сумма квадратов долей всех фирм, действующих на рынке:

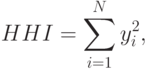
$HHI = \sum\limits_{i = 1}^N {y_i^2 } ,$

где HHI - индекс Херфиндаля-Хиршмана; $y_i = \frac{{q_i }} {Q}$ - доля производства (продаж) i-й фирмы в общем объеме выпуска (сбыта) отрасли; N - число фирм в отрасли.

Значения y_i могут быть выражены в долях либо в процентах:

$\begin{gathered} 0 < HHI \leq 1, \hfill \\ 0 < HHI \leq 10000. \hfill \\ \end{gathered}$

Чем меньшие значения принимает индекс Херфиндаля-Хиршмана, тем сильнее конкуренция на рынке, меньше концентрация и слабее рыночная власть фирм. Определение уровня концентрации по двум показателям приведено в таблице 3.2.

Таблица 3.2.
Показатель	Концентрация
Показатель	низкая	средняя	высокая
Индекс концентрации CR₃	менее 45%	45%-70%	70%-100%
Индекс Херфиндаля-Хиршмана	менее 1000	1000-2000	2000-10000

Сравним уровни концентрации производства в промышленности России и Германии в конце 1990-х гг^{2Концентрация производства: условия, факторы, политика / Под ред. А.Е. Шас-титко; Бюро экон. анализа. М.: ТЕИС, 2001.}. Как видно из таблицы 3.3, большинство отраслей российской промышленности характеризовались высокой и средней концентрацией, в то время как для промышленности Германии отмечался низкий уровень концентрации. Исключение составляют некоторые отрасли пищевой промышленности. Нельзя не сделать вывода о неадекватности структуры промышленного производства в России и Германии. Основная причина этого - формирование послевоенной германской промышленности в условиях открытого рынка. Однако можно наблюдать, что в целом соотношение уровней концентрации между отраслями сохраняется для обеих стран: более низкая концентрация в пищевых отраслях и более высокая - в химическом и машиностроительном производствах.

Таблица 3.3.
Отрасль	Германия, HHI	Россия, HHI
Добыча торфа	93	924
Лесная индустрия	11	284
Первичная обработка алюминия	110	3174
Химико-фармацевтическая	128	1412
Производство неорг. удобрений	291	1500
Производство стальных труб	76	1561
Производство автомобилей	160	1684
Производство приборов связи	109	312
Производство игрушек	47	519
Молочная промышленность	15	19
Сахарная промышленность	184	184
Переработка мяса	6	75

3. Дисперсия рыночных долей

Дисперсия определяется как отклонения рыночных долей всех фирм рынка:

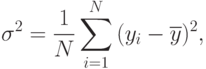
$\sigma ^2 = \frac{1} {N}\sum\limits_{i = 1}^N {(y_i - \overline y )^2 } ,$

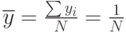где $\overline y = \frac{{\sum {y_i } }} {N} = \frac{1} {N}$ — средняя рыночная доля; N — число фирм в отрасли.

Показатель дисперсии измеряется в абсолютных значениях и может принимать любые значения. Он характеризует возможную рыночную власть фирм через неравенство их размеров. Чем больше величина дисперсии, тем более неравномерным и, следовательно, более концентрированным является рынок, тем слабее конкуренция и тем сильнее власть крупных фирм на рынке.

Между индексом Херфиндаля-Хиршмана и дисперсией наблюдается следующее соотношение:

$HHI = N\sigma ^2 + \frac{1} {N},$

так что при неизменном числе фирм более высокая дисперсия, т.е. усиление неравномерности распределения долей рынка, приводит к увеличению концентрации.

4. Коэффициент Джини

Коэффициент Джини определяется как процентная доля размера отрасли, приходящаяся на процентное число фирм, действующих на рынке:

где G - коэффициент Джини; D - кумулятивный процент размера отрасли (рынка); N - кумулятивный процент числа фирм на рынке.

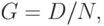
Максимальное значение коэффициента, равное единице, свидетельствует о ситуации абсолютного неравенства (на одну фирму приходится весь объем выпуска отрасли). Минимальное значение показателя, равное нулю, означает абсолютное равенство: каждая фирма производит одинаковую долю отрасли (или одинаковый процент фирм производит одинаковый процент совокупного выпуска).

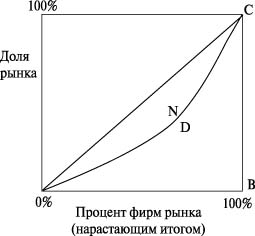
Коэффициент Джини иллюстрируется кривой Лоренца (рис. 3.1).

Рис. 3.1. Кривая Лоренца

Кривая ANC - кривая Лоренца - показывает, какая процентная доля рынка приходится на каждый процент фирм, действующих на рынке. При этом коэффициент Джини определяется как отношение площади фигуры D к площади треугольника ABC. При абсолютном равенстве кривая Лоренца приобретает вид биссектрисы - прямой АС, площадь фигуры D становится равной нулю, следовательно, и коэффициент Джини оказывается равным нулю. При абсолютном неравенстве кривая Лоренца совпадает с линией ABC, площади D и ABC также совпадают, коэффициент Джини оказывается равным единице.

Данный показатель, однако, обладает существенным недостатком: он измеряет только относительные размеры фирм; его значение будет одним и тем же для трех одинаковых фирм рынка и для десяти, хотя, очевидно, степени конкуренции для трех и для десяти фирм различны.

5. Индекс Холла-Тайдмана

Индекс Холла-Тайдмана рассчитывается на основе сопоставления рангов фирм рынка следующим образом:

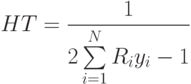
$HT = \frac{1} {{2\sum\limits_{i = 1}^N {R_i y_i - 1} }}$

где НТ - индекс Холла-Тайдмана; R_i - ранг фирмы на рынке (самая крупная фирма имеет ранг 1); y_i - доля фирмы.

Максимальное значение индекса Холла-Тайдмана равно единице (в условиях монополии). Минимальное значение равно 1/N, N - число фирм в отрасли. По своему действию данный показатель сходен с индексом Херфиндаля-Хиршмана, однако к достоинствам индекса Холла-Тайдмана следует отнести возможность ранжировать фирмы по степени значимости, что способствует более глубокому анализу отрасли.

Дальше >>

Микроэкономика фирмы

Микроэкономика фирмы