| Азербайджан |
Методы генерации признаков
11.6. Признаки формы и размера
Рассмотрим методы генерации признаков, описывающих структуру. Существует два основных пути описания формы:
- Полное описание формы в регенеративной манере (например, признаки Фурье). По такому описанию полностью можно восстановить образ.
- Не восстановительное описание формы (дескриптивные признаки). По такому описанию можно отличить заданную форму от других, но не полностью восстановить образ.
11.6.1. Признаки Фурье
Отметим, что полное описание позволяет восстанавливать границу образа. Частичное же описание дает признаки для распознавания. Нас интересует вопрос о зависимости изменения признаков от преобразований.
Пусть  , где
, где  ,
– координаты последовательных точек границы;
,
– координаты последовательных точек границы;  – комплексные числа.
Для
– комплексные числа.
Для  точек
точек 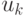 определим ДФП (DFT):
определим ДФП (DFT):

где  – Фурье-описание границы.
– Фурье-описание границы.
Рассмотрим, как изменяется  при сдвиге, повороте,
масштабировании и сдвиге начальной точки.
при сдвиге, повороте,
масштабировании и сдвиге начальной точки.
Сдвиг описывается следующим образом:  ,
,  и
и  . Тогда
. Тогда

При  , т.к.
, т.к.

При  , т.к.
, т.к.

Поворот описывается следующим соотношением:  .
Следовательно,
.
Следовательно,  ,
т.е. поворот не меняет модулей, а именно
,
т.е. поворот не меняет модулей, а именно  .
.
Масштабирование описывается следующим соотношением:  .
Следовательно,
.
Следовательно,  . Т.к.
. Т.к.


Сдвиг начальной точки определяется следующим образом:  . Следовательно
. Следовательно

 .
.11.6.2. Цепной код
Определение. Цепным кодом называется кодирование (запоминание) последовательности поворота вектора по пикселям на границе описываемой области – маршрута обхода.
Из построенного цепного кода конструируются следующие признаки:
- относительная доля каждого направления,
- относительная доля разных сочетаний кривизны.
Недостатком представления изображения цепным кодом является появления шума. Способом борьбы с данным недостатком является использование более мелкой (точной) сетки.
11.6.3. Геометрические свойства фигуры
Пусть  – периметр фигуры,
– периметр фигуры,  – площадь
фигуры. Рассмотрим следующие свойства: некруглость фигуры и энергию
изгиба.
– площадь
фигуры. Рассмотрим следующие свойства: некруглость фигуры и энергию
изгиба.
11.6.3.1. Некруглость фигуры определяется по следующей формуле:

Рассмотрим два крайних значения для данного свойства. Наиболее лучшее (наибольшая "круглость") значение должно быть для круга, оно равно

Более худший вариант (меньшая "круглость") наблюдается у квадрата. Соответствующее значение равно

11.6.3.2. Энергия изгиба. Пусть задано  точек фигуры. Тогда Энергия изгиба описывается следующей формулой:
точек фигуры. Тогда Энергия изгиба описывается следующей формулой:

 и
и  .
. 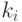 характеризует изменение угла в вершине.
характеризует изменение угла в вершине.11.6.4. Скелетизация
Определение. Скелетизацией называется построение скелета, описывающего форму фигуры.
Определение. Скелетом называется множество всех центров вписанных в фигуру максимальных окружностей.
MAT (Medial Area Transform) определяется как скелет плюс функция ширины фигуры.