| Азербайджан |
Методы генерации признаков
11.2. Преобразование Карунена-Лоева
Пусть  – вектор измерений образа. Целью
преобразования является построение такого вектора признаков, что
– вектор измерений образа. Целью
преобразования является построение такого вектора признаков, что
![E\left[y(i)y(j)\right]=0\text{ при } i\neq j.](/sites/default/files/tex_cache/3afd70670e55fdbc7c8e16b5c13cfa89.png)
Пусть
Будем считать, что
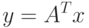
Обозначим ![R_y=E\left[yy^T\right]](/sites/default/files/tex_cache/4f18036164a184326fa173b373fb62f1.png) , тогда
, тогда
![R_y=E\left[yy^T\right]=E\left[A^T xx^T A\right]=A^T R_x A,](/sites/default/files/tex_cache/61a4e7b8432189f3a12785c8d8277784.png)
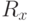 – симметричная матрица и ее собственные вектора ортогональны.
– симметричная матрица и ее собственные вектора ортогональны.Выберем в качестве  собственные вектора матрицы
собственные вектора матрицы 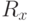 .
Тогда
.
Тогда 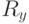 – диагональная матрица, у которой на диагонали стоят собственные
значения
– диагональная матрица, у которой на диагонали стоят собственные
значения 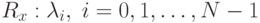 . Таким образом
. Таким образом
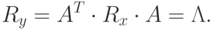
Если 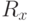 положительно определенная матрица, то собственные значения
положительно определенная матрица, то собственные значения 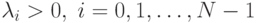 .
.
Описанное преобразование называется преобразованием Карунена-Лоева. Оно имеет фундаментальное значение, т.к. оно приводит к построению некоррелированных признаков.
11.2.1. Свойства преобразования Карунена-Лоева
Пусть 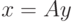 или
или 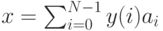 – разложение по базисным векторам.
– разложение по базисным векторам.
Определим новый  -мерный вектор
-мерный вектор 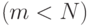 :
:
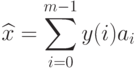
 – проекция
– проекция  на подпространство. Если мы аппроксимируем
на подпространство. Если мы аппроксимируем  с
помощью
с
помощью  , то ошибка есть (выбираем те векторов,
, то ошибка есть (выбираем те векторов,  для которых ошибка
минимальна):
для которых ошибка
минимальна):![\begin{aligned}
&E\|x-\widehat{x}\|^2=E
\left[
\left\|
\sum_{i=0}^{N-1}y(i)a_i
\right\|^2
\right]
=E
\left[
\sum_i\sum_j(y(i)a_i^T)(y(i)a_i)
\right]=\\
&=\sum_{i=m}^{N-1}E
\left[
y^2(i)
\right]
=\sum_{i=m}^{N-1}a_i^T E
\left[
xx^T
\right]
a_i=\sum_{i=m}^{N-1}a_i^T\lambda_i a_i =\sum_{i=m}^{N-1}\lambda_i.
\end{aligned}](/sites/default/files/tex_cache/dba30782718e5eb7eca97f87458d14cc.png)
Тогда очевидно, что выбирать нужно  базисных векторов с
максимальными собственными значениями.
базисных векторов с
максимальными собственными значениями.
Отметим еще раз соотношение преобразования Карунена-Лоева с методом селекции признаков. В методе селекции признаков в качестве критерия выступали дискриминантные свойства полученного вектора признаков. В преобразовании Карунера-Лоева в качестве критерия выступает наилучшее приближение исходных измерений.
11.2.2. Применение преобразования Карунена-Лоева к задаче классификации. В данном случае основная концепция заключается в том, что подпространство главных собственных значений может быть использовано для классификации.
- для каждого класса
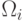 строим корреляционную матрицу
строим корреляционную матрицу 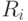 ,
, - выбираем
 главных собственных значений и собственных векторов,
главных собственных значений и собственных векторов, - строим соответствующие матрицы
 , у которых столбцы – значения собственных векторов.
, у которых столбцы – значения собственных векторов. - неизвестный (пробный) вектор
 классифицируем по правилу
классифицируем по правилу 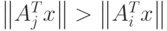 при
при 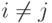 , т.е. в ближайшее подпространство.
, т.е. в ближайшее подпространство.
11.2.3. Декомпозиция сингулярных значений.
Пусть задана матрица  ранга
ранга  . Покажем, что существуют такие
унитарные матрицы
. Покажем, что существуют такие
унитарные матрицы 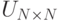 и
и  , что
, что
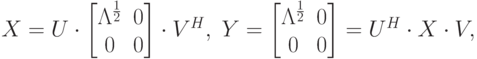
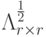 – диагональная матрица с элементами
– диагональная матрица с элементами 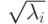 и
и 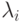 –
–  ненулевых
собственных значений матрицы
ненулевых
собственных значений матрицы 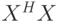 . Иначе существуют такие унитарные
матрицы
. Иначе существуют такие унитарные
матрицы 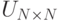 и
и  , что преобразованная
, что преобразованная  путем
путем 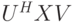 есть диагональная матрица. Следовательно
есть диагональная матрица. Следовательно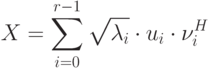 |
( 11.2) |
 и
и 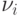 – первые
– первые  столбцов матриц
столбцов матриц 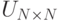 и
и  соответственно, т.е.
соответственно, т.е.  и
и 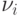 – собственные вектора матриц
– собственные вектора матриц 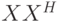 и
и 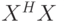 соответственно.
соответственно.Собственные значения 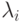 называются сингулярными
значениями матрицы
называются сингулярными
значениями матрицы  . Преобразование (11.2) – преобразование сингулярных значений или
спектральное представление
. Преобразование (11.2) – преобразование сингулярных значений или
спектральное представление  .
.
Если  аппроксимировать следующим образом
аппроксимировать следующим образом
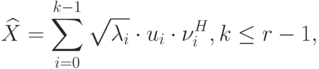
 есть сумма
есть сумма  одноранговых матриц и имеет
ранг равный
одноранговых матриц и имеет
ранг равный  . Можно показать, что квадратичная ошибка
. Можно показать, что квадратичная ошибка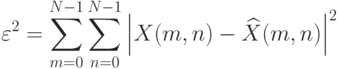
 -ранговых матриц. Ошибка аппроксимации есть
-ранговых матриц. Ошибка аппроксимации есть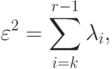
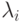 .
.Таким образом,  есть наилучшая аппроксимация в смысле нормы
Фробениуса. Данная аппроксимация напоминает преобразование Карунена-Лоева.
есть наилучшая аппроксимация в смысле нормы
Фробениуса. Данная аппроксимация напоминает преобразование Карунена-Лоева.

 и
и