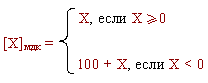Модифицированные коды

Важная особенность рассмотренных кодов состоит в том, что в процессе выполнения операции сложения-вычитания не происходит переполнения цифровой части числа и переноса в знаковый разряд. Переполнение возникает лишь в знаковом разряде. Так бывает потому, что сумма двух слагаемых по модулю меньше единицы.

При решении реальных задач часто трудно определить заранее, будет ли сумма двух слагаемых меньше единицы. Во всяком случае, для предотвращения переполнения можно вводить дополнительные ограничения на величину слагаемых, сужающих диапазон чисел, с которыми оперирует машина. И то, и другое является неприемлемым.

Рассмотрим такой пример:

X = -0,101   Дополнительный код  1.011 = [X]дк
Y= -0,111                        1.001 = [Y]дк
S- = X- + Y-                      0.100 = [S]дк

То есть получаем неправильный результат как по знаку, так и в цифровой части.

Рассмотрим ещё один пример:

X = +0,101   В любом из ранее рассмотренных   0.101 = [X]дк,ок
Y = +0,111   кодов имеем                      0.111 = [Y]дк,ок
S+ = X+ + Y+                                   1.100 = [S]дк,ок

То есть и в этом случае происходящее переполнение в цифровой части искажает результат операции.

Можно заметить, что переполнение числовой сетки происходит в случае одинаковых знаков слагаемых, так как именно в этом случае модуль результата превосходит модули каждого из слагаемых, сам факт переполнения может быть зафиксирован изменением знака результата.

Таким образом, одним из способов фиксации переполнения является автоматическое определение перехода от одинаковых знаков слагаемых к противоположному знаку результата.

Однако такой способ фиксации переполнения неудобен, так как предварительно знаки слагаемых должны быть запомнены, сравнены между собой и после получения результата.

Существует другой принцип фиксации переполнения. Этот принцип основан на применении так называемых модифицированных кодов. Очевидно,что при переполнении разрядной сетки вычисления необходимо прекратить или, по крайней мере, выработать специальный признак переполнения, а решение о прекращении вычислений возложить на программиста.

Существо модифицированных кодов состоит в том, что к знаковому разряду добавляется ещё один разряд:

" + " ставится в соответствие 00

" – " ставится в соответствие 11

Тогда, по определению модифицированным дополнительным кодом числа называется

Возникающий в знаковых разрядах перенос теряется. В целом же модифицированный код не отличается от простого дополнительного. Аналогично, по определению, обратным кодом является:

Как и в случае простого обратного кода, возникающая единица переноса в знаковых разрядах по цепи циклического переноса добавляется в младший разряд цифровой части числа.

Так как в сложении по-прежнему участвуют только числа меньше единицы, то

S = X + Y < 2

Поэтому старший знаковый разряд не может быть искажён переносом из цифровой части числа, с другой стороны, перенос, возникающий при сложении чисел в случае, когда

S = X + Y > 1

искажает младший знаковый разряд.

Несовпадение знаковых разрядов после выполнения операции указывает на факт наличия переполнения.

При этом различают два типа переполнения:

• " 01 " - положительное
• " 10 " - отрицательное.

Первому ставится в соответствие комбинация 01 в знаковых разрядах, а второму – 10.

Примеры

Модифицированный дополнительный код:

а) [X]мдк = 00.101            +00.101
   [Y]мдк = 00.111             00.111
                      [S]мдк = 01.100 – положительное переполнение

б) [X]мдк = 11.101            +11.101
   [Y]мдк = 11.001             11.001 
                    [S]мдк = 1х10.110 – отрицательное переполнение

Модифицированный обратный код

а) [X]мок = 00.101            +00.101
   [Y]мок = 00.111             00.111 
                      [S]мок = 01.100 – положительное переполнение 

б) [X]мок = 11.010            +11.010
   [Y]мок = 11.000             11.000 
                            1|10.010
                             ------>1
                      [S]мок = 10.011 – отрицательное переполнение