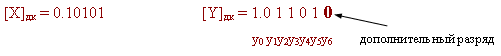Модифицированные коды

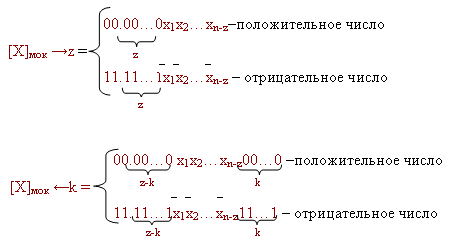
Если чисто формально сделать преобразование выражения некоторого числа, записанного в прямом коде до выполнения сдвига и после выполнения микрооперации сдвига, в обратный модифицированный код, то:

То есть при сдвиге вправо отрицательного числа старшие разряды заполняются единицами. При сдвиге влево в старшие и младшие разряды пишутся единицы.

Пользуясь аналогичными правилами, нетрудно установить, что при сдвиге влево отрицательного числа в модифицированном дополнительном коде младшие разряды сдвинутого числа нужно заполнить нулями.

Умножение с младших разрядов в дополнительном коде

Алгоритм:

[Z]дк = (...(0+[X]дк*[yn+1 – yn])*2-1 + [X]дк*[yn – yn-1])*2-1 + ...
... + [X]дк*[y2 – y1])*2-1 + [X]дк*[y1 – y0]

Если y_n = y_{n+ 1} , то производится сдвиг частичного произведения.

Если y_n = 0 и y_n+1 = 1, то к частичному произведению прибавляется [X]_дк

Если y_n = 1 и y_n+1 = 0, то из частичного произведения вычитается [X]_дк.

Пример:

Умножение со старших разрядов в дополнительном коде

[Z]дк = [X]дк*[Y]дк = [X]дк*(y1 – y0 ) + [X]дк*(y2 – y1 )*2-1 + ... +
   + [X]дк*(yn+1 – yn )*2-n

[-X]дк = 1.01011 
[Z]дк = [-X]дк + [X]*2-1 + [X]дк*2-2*0 + [-X]дк*2-3 + 
     + [X]дк*2-4 + [-X]дк*2-5

+1.01011       [-X]дк                  
 0.010101      [X]дк*2-1
 ________ 
 +1.101011 
 1.11101011    [-X]дк*2-3
 __________ 
 +1.10010111 
 0.000010101   [X]дк*2-4
 ___________ 
 +1.101000011 
 1.1111101011 [-X]дк*2-5
 ____________ 
 1.1001110001 
Ответ: [Z]дк = 1.1001110001