Способы представления чисел в ЭВМ
Как мы уже знаем, применяются два основных способа представления чисел - с фиксированной и плавающей запятой. Большинство универсальных ЭВМ работает с числами, представленными с плавающей запятой, а большинство специализированных - с фиксированной запятой.
Однако целый ряд машин работает с числами в этих двух форматах.
В общем виде способ представления чисел сильно влияет на характер программирования. Так, программирование для ЭВМ, работающих в системе с фиксированной запятой, значительно усложняется, поскольку помимо алгоритмических трудностей этот процесс требует ещё отслеживания положения запятой.
Фиксированная запятая
Оговоримся, что разрядная сетка машины имеет постоянное число разрядов - n.
При представлении чисел с фиксированной запятой считают, что запятая всегда находится перед старшим разрядом, а все числа, которые участвуют в вычислениях, считаются по абсолютной величине меньше единицы:
|X| < 1
Введём две характеристики чисел: диапазон изменения и точность представления.
Диапазон изменения характеризуется теми пределами, в которых могут находиться числа, с которыми оперирует машина.
Отличное от нуля самое малое число:
Таким образом, диапазон чисел, с которыми работает ЭВМ, есть:
|X|min <= |X| <= |X|max
2-n <= |X| <= 1 - 2-n
Иными словами, числа, которые выходят за диапазон изменения, в ЭВМ не могут быть представлены точно. Если
|X| < |X|min = 2-n,
то такое число воспринимается как нуль.
Если:
|X| > |X|max = 1- 2-n,
то такое число воспринимается как бесконечно большое. Этим двум случаям соответствуют понятия машинного нуля и машинной бесконечности.
При оптимальном округлении абсолютная ошибка:
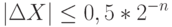
Минимальная относительная ошибка:
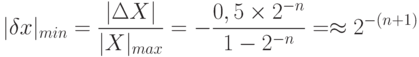
так как 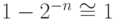 при большом " n "
при большом " n "
Максимальная относительная ошибка:

Ошибка представления числа зависит от величины самого числа и способа округления:

Заметим, что для малых чисел ошибка может достигать большой величины.


