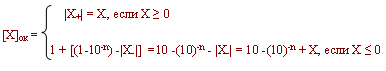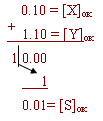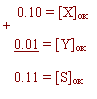Способы представления чисел в ЭВМ

Обратный код

Обратным называется код, для которого в знаковом разряде положительного числа пишется "0", в цифровых - модуль числа, а для отрицательного - в знаковом разряде пишется единица, в цифровых - инвертированные разряды исходного числа.

Определим диапазоны чисел:

X_{+ min} = 0,00...0 - положительный нуль.

X_{+ max} = 0,111...1 = 1 - 2^-n

X_{- min} = 1,11...1 0 = 2 - 2^-n+1

X_{- max} = 1,00...00 = 1

В обратном коде есть два изображения нуля:

"Положительный" нуль:

[X]ок = 0,0...0

и "отрицательный" нуль:

[X]ок = 1,11...11

При этом

X - X = [X+]ок + [X-]ок = |X+| + 10 - (10)-n - |X-| = +10 - (10)-n = 0

То есть, единица переноса в знаковом разряде эквивалентна единице младшего разряда. Поэтому при выполнении операции сложения-вычитания необходимо возникающий перенос циклически прибавлять в младший разряд частичного результата.

Рассмотрим прежние четыре случая, помня о том, что сумма двух слагаемых по модулю должна быть меньше единицы.

1. X+ = 0,10
   Y- = -0,01			              	            
   X+ + Y- = S+

   В обратном коде:

   

   
   

   Возникающее переполнение должно быть добавлено к младшему разряду частичной суммы.

2. X+ = 0,10
   Y+ = +0,01
   X+ + Y+  = S+

   В обратном коде:

   

   
   

   Нет никаких особенностей по сравнению с прямым кодом.

3. X+ = 0,01
   Y- = -0,10
   X+ + Y- = S-

   В обратном коде:

   

   
   

   То есть, не возникает циклического переноса.

4. X- = -0,01					         
   Y- = -0,10					       
   X- + Y- = S-

   В обратном коде:

   

   
   

Возникает переполнение знакового разряда, которое добавляется в младший разряд частичной суммы.

Заметим, что получение обратного кода проще, чем дополнительного. Это поразрядно выполняемая микрооперация инверсии кода. Как станет ясно из схемного решения, эта микрооперация выполняется так же быстро, как и передача кода.

Поскольку результатом операции является совокупность результатов по всем разрядам, то данную операцию можно выполнять одновременно над всеми цифровыми разрядами числа.