Производящие функции и рекуррентные соотношения
Теория производящих функций тесно связана с рекуррентными соотношениями.
Вернемся снова к делению многочленов. Пусть функции  и
и 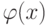 разложены в степенные ряды,
разложены в степенные ряды,
- два многочлена, причем

. Мы будем, кроме того,
предполагать, что

, то есть, что алгебраическая дробь

правильна (в противном случае мы всегда можем выделить
из нее целую часть). Мы знаем, что если
 |
(
10.10)
|
то
Раскроем в правой части этого равенства скобки и сравним
коэффициенты при
одинаковых степенях

слева и справа. Сначала мы получим

соотношений такого вида:
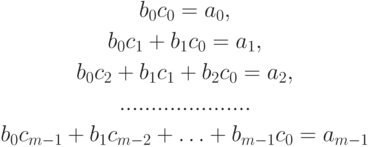 |
(
10.11)
|
(если
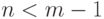
, то мы считаем, что
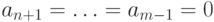
). А дальше все соотношения имеют один и тот же вид:
 |
(
10.12)
|
(ведь в

нет членов, содержащих
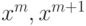
и
т.д.). Таким образом,
коэффициенты 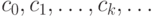
ряда
(10.10) удовлетворяют рекуррентному соотношению (10.12).
Коэффициенты этого
соотношения зависят лишь от знаменателя дроби.
Числитель же дроби нужен для
нахождения первых членов
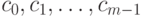
рекуррентной
последовательности.
Обратно, если дано рекуррентное соотношение (10.12) и заданы члены 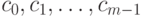 , то мы сначала по формулам (10.11) вычислим
значения
, то мы сначала по формулам (10.11) вычислим
значения 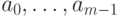 . А тогда производящей функцией для
последовательности чисел
. А тогда производящей функцией для
последовательности чисел 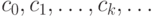 является
алгебраическая дробь
является
алгебраическая дробь
 |
(
10.13)
|
На первый взгляд кажется, что мы мало выиграли при замене рекуррентного
соотношения производящей функции. Ведь все равно придется делить
числитель на
знаменатель, а это приведет к тому же самому рекуррентному соотношению
(10.12). Но дело в том, что над дробью (10.13) можно выполнять некоторые
алгебраические
преобразования, а это облегчит отыскание чисел
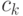
.
Об едином нелинейном рекуррентном соотношении
При решении задачи о разбиении последовательности мы пришли к
рекуррентному соотношению
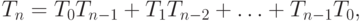 |
(
10.14)
|
где

.Покажем, как решить соотношение (10.14). Для этого составим производящую
функцию.
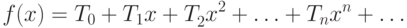 |
(
10.15)
|
Положим
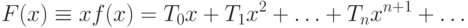 |
(
10.16)
|
и возведем

в квадрат. Мы получим, что
Но по рекуррентному соотношению (10.14),
Значит,
Полученный ряд есть не что иное, как

; поскольку

, он равен
Для функции

получилось квадратное уравнение (10.17). Решая его, находим, что
Мы выбрали перед корнем знак минус, так как в противном случае при
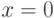
мы имели бы
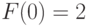
, а из разложения (10.16) видно, что
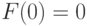
.
 и
и 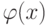 разложены в степенные ряды,
разложены в степенные ряды,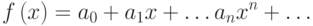
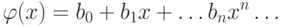
 . Мы будем, кроме того,
предполагать, что
. Мы будем, кроме того,
предполагать, что  , то есть, что алгебраическая дробь
, то есть, что алгебраическая дробь  правильна (в противном случае мы всегда можем выделить
из нее целую часть). Мы знаем, что если
правильна (в противном случае мы всегда можем выделить
из нее целую часть). Мы знаем, что если
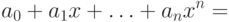
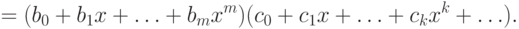
 слева и справа. Сначала мы получим
слева и справа. Сначала мы получим  соотношений такого вида:
соотношений такого вида: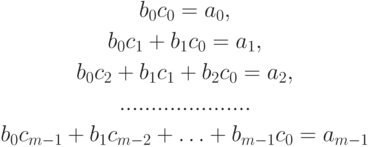
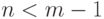 , то мы считаем, что
, то мы считаем, что 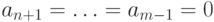 ). А дальше все соотношения имеют один и тот же вид:
). А дальше все соотношения имеют один и тот же вид:
 нет членов, содержащих
нет членов, содержащих 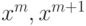 и
т.д.). Таким образом, коэффициенты
и
т.д.). Таким образом, коэффициенты 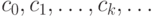 ряда
(10.10) удовлетворяют рекуррентному соотношению (10.12). Коэффициенты этого
соотношения зависят лишь от знаменателя дроби. Числитель же дроби нужен для
нахождения первых членов
ряда
(10.10) удовлетворяют рекуррентному соотношению (10.12). Коэффициенты этого
соотношения зависят лишь от знаменателя дроби. Числитель же дроби нужен для
нахождения первых членов 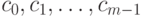 рекуррентной
последовательности.
рекуррентной
последовательности.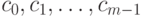 , то мы сначала по формулам (10.11) вычислим
значения
, то мы сначала по формулам (10.11) вычислим
значения 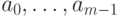 . А тогда производящей функцией для
последовательности чисел
. А тогда производящей функцией для
последовательности чисел 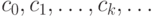 является
алгебраическая дробь
является
алгебраическая дробь
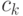 .
.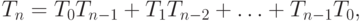
 .Покажем, как решить соотношение (10.14). Для этого составим производящую
функцию.
.Покажем, как решить соотношение (10.14). Для этого составим производящую
функцию.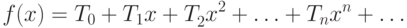
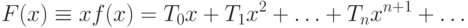
 в квадрат. Мы получим, что
в квадрат. Мы получим, что
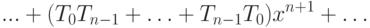
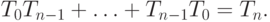
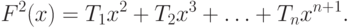
 ; поскольку
; поскольку  , он равен
, он равен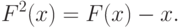
 получилось квадратное уравнение (10.17). Решая его, находим, что
получилось квадратное уравнение (10.17). Решая его, находим, что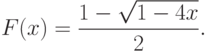
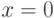 мы имели бы
мы имели бы 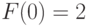 , а из разложения (10.16) видно, что
, а из разложения (10.16) видно, что 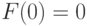 .
.
