| Россия |
Целые и последовательности (последовательное распределение)
Введение
Большинство вычислительных устройств в качестве основных объектов допускает только двоичные наборы, целые и символы, поэтому, прежде чем работать с более сложными объектами, их необходимо представить двоичными наборами, целыми или символами. Например, числа с плавающей запятой кодируются целыми - мантиссой и порядком этого числа, но такое кодирование обычно незаметно для пользователя. В противоположность этому, рассмотренные во второй и третьей лекции способы кодирования объектов (множества, последовательности, деревья) всегда адресованы пользователю.
Любой заданный класс объектов может иметь несколько возможных представлений, и выбор наилучшего из них решающим образом зависит от того, каким образом объект будет использован, а также от типа производимых над ним операций. Поэтому рассмотрим не только свойства самих представлений, но также и некоторые приложения.
Целые
Целые являются основными объектами в вычислительной комбинаторике. В различных вычислительных теоретико-числовых исследованиях изучаются сами целые числа, но мы будем использовать их главным образом при подсчете и индексировании. В последнее время установлено, что полезны различные представления. В этой лекции обсудим общий класс позиционных представлений.
Мы будем рассматривать только неотрицательные целые. Кроме того, к любому представлению неотрицательных целых легко присоединить одиночный знаковый двоичный разряд.
Позиционные системы для представления целых чисел очень широко известны,
поскольку они встречаются во многих разделах математики, начиная с "новой
математики" и кончая углубленным курсом теории чисел. В системе счисления
с основанием  каждое положительное целое число имеет
единственное представление в виде конечной последовательности
каждое положительное целое число имеет
единственное представление в виде конечной последовательности
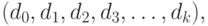 |
( 2.1) |
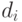 - целое, удовлетворяющее условию
- целое, удовлетворяющее условию  и
и 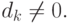 Нуль представляется последовательностью
Нуль представляется последовательностью 
 называется основанием системы
называется основанием системы  Целое, соответствующее последовательности (2.1), имеет вид
Целое, соответствующее последовательности (2.1), имеет вид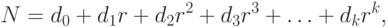
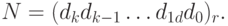
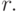 Например, древние вавилоняне использовали
Например, древние вавилоняне использовали 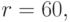 а индейцы племени Майя —
а индейцы племени Майя — 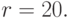 Сегодня наиболее широко используется
Сегодня наиболее широко используется 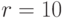 - десятичная система, которую мы унаследовали от арабов, и
- десятичная система, которую мы унаследовали от арабов, и 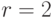 - двоичная система, которая лежит в основе современных вычислительных устройств. В действительности она применяется лишь на самом низком уровне аппаратного оборудования; в сложных вычислительных
устройствах и базисных языках удобнее использовать
- двоичная система, которая лежит в основе современных вычислительных устройств. В действительности она применяется лишь на самом низком уровне аппаратного оборудования; в сложных вычислительных
устройствах и базисных языках удобнее использовать  или
или 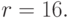
Единственность этого представления можно доказать методом от противного.
Числа 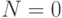 и
и 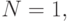 очевидно, имеют единственное
представление. Предположим, что представление не единственно, и пусть
очевидно, имеют единственное
представление. Предположим, что представление не единственно, и пусть  будет наименьшим целым числом, имеющим два различных представления:
будет наименьшим целым числом, имеющим два различных представления:
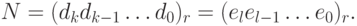
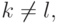 то без потери общности предположим, что
то без потери общности предположим, что  Тогда, поскольку
Тогда, поскольку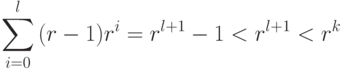
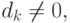 мы заключаем, что
мы заключаем, что |
( 2.2) |
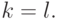 Аналогично,
если
Аналогично,
если  мы имели бы снова неравенство (2.2) и отсюда
с необходимостью
мы имели бы снова неравенство (2.2) и отсюда
с необходимостью  Следовательно, число
Следовательно, число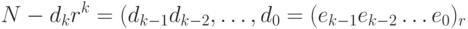
 - наименьшее из таких чисел.
- наименьшее из таких чисел.Для доказательства того, что каждое положительное целое имеет представление
по основанию 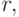 достаточно задать алгоритм, конструирующий (с
необходимостью единственное) представление данного числа
достаточно задать алгоритм, конструирующий (с
необходимостью единственное) представление данного числа 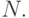
Алгоритм 1. Преобразование числа  в его представление
в его представление 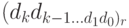 в системе счисления с основанием
в системе счисления с основанием  .
.
Он строит последовательность 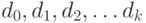 путем
повторения деления на
путем
повторения деления на  и записи остатков. Пусть на первом шаге при
делении
и записи остатков. Пусть на первом шаге при
делении  на
на  остаток будет
остаток будет 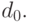 Частное,
полученное в результате первого шага, делим на
Частное,
полученное в результате первого шага, делим на 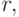 вновь полученное частное делим на
вновь полученное частное делим на  и так далее. Полученная в
результате такого процесса последовательность остатков и будет требуемым
представлением
и так далее. Полученная в
результате такого процесса последовательность остатков и будет требуемым
представлением  по основанию
по основанию 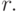
Важным обобщением систем счисления с основанием  являются смешанные системы счисления, в которых задается не единственное основание
являются смешанные системы счисления, в которых задается не единственное основание 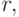 а последовательность оснований
а последовательность оснований  , и последовательность
(2.2) соответствует целому
, и последовательность
(2.2) соответствует целому
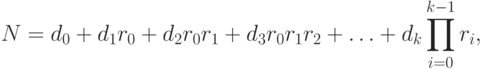
 удовлетворяет
неравенству
удовлетворяет
неравенству 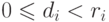 и
и  если
если 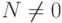 - тот факт, что каждая такая
последовательность соответствует единственному числу и каждое положительное целое число имеет единственное представление, следует из простого обобщения результатов для обычных систем счисления, которые являются частным случаем смешанных систем при
- тот факт, что каждая такая
последовательность соответствует единственному числу и каждое положительное целое число имеет единственное представление, следует из простого обобщения результатов для обычных систем счисления, которые являются частным случаем смешанных систем при 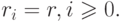
Смешанные системы счисления могут вначале показаться странными, но в действительности в повседневной жизни они встречаются почти так же часто, как и десятичные.
Пример. Рассмотрим нашу систему измерения времени: секунды, минуты, часы,
дни недели и годы. Это - в точности смешанная система с 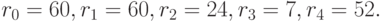
Представление целого  в смешанной системе
счисления
в смешанной системе
счисления 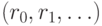 осуществляется с помощью алгоритма 2, который является простым обобщением алгоритма 1. Вместо того, чтобы для получения
осуществляется с помощью алгоритма 2, который является простым обобщением алгоритма 1. Вместо того, чтобы для получения 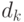 в качестве делителя всегда использовалась
в качестве делителя всегда использовалась 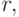 в алгоритме 2 используется
в алгоритме 2 используется 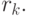
Алгоритм 2. Преобразование числа  в его
представление
в его
представление 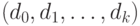 в смешанной системе счисления
в смешанной системе счисления 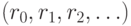 .
.
Последовательности
Бесконечная последовательность
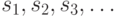
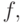 областью определения которой является
множество положительных целых чисел:
областью определения которой является
множество положительных целых чисел:  Во
многих случаях индексирование последовательности более удобно начинать с нуля; тогда областью определения
Во
многих случаях индексирование последовательности более удобно начинать с нуля; тогда областью определения  будет множество целых неотрицательных чисел.
Аналогично определим конечную последовательность или список
будет множество целых неотрицательных чисел.
Аналогично определим конечную последовательность или список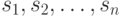
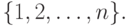 Примером бесконечной последовательности являются простые числа
Примером бесконечной последовательности являются простые числа |
( 2.3) |
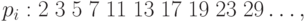
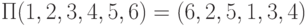
В комбинаторных алгоритмах часто приходится встречаться с представлениями конечных последовательностей (или начальных сегментов бесконечных последовательностей ) и операциями над ними.
