| Россия |
Алгоритмы рекуррентных соотношений
Решение рекуррентных соотношений
Будем говорить, что рекуррентное соотношение имеет порядок  ,
если оно позволяет выразить
,
если оно позволяет выразить 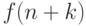 через
через 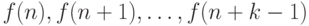 . Например,
. Например,
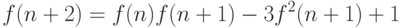
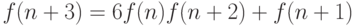
 -го порядка, то ему
удовлетворяет бесконечно много последовательностей. Дело в том, что первые
-го порядка, то ему
удовлетворяет бесконечно много последовательностей. Дело в том, что первые  элементов последовательности можно задать совершенно произвольно - между
ними нет никаких соотношений. Но если первые
элементов последовательности можно задать совершенно произвольно - между
ними нет никаких соотношений. Но если первые  элементов
заданы, то все остальные элементы определяются совершенно однозначно - элемент
элементов
заданы, то все остальные элементы определяются совершенно однозначно - элемент 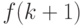 выражается в силу рекуррентного соотношения через
выражается в силу рекуррентного соотношения через 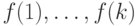 элемент
элемент 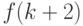 - через
- через 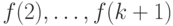 и т.д.
и т.д.Пользуясь рекуррентным соотношением и начальными членами, можно один за
другим выписывать члены последовательности, причем рано или поздно получим
любой ее член. Однако при этом придется выписать и все предыдущие члены -
ведь не узнав их, мы не узнаем и последующих членов. Но во многих случаях нужно
узнать только один определенный член последовательности, а остальные не нужны. В этих
случаях удобнее иметь явную формулу для  -го члена
последовательности. Некоторая последовательность является решением данного рекуррентного соотношения,
если при подстановке этой последовательности соотношение тождественно выполняется. Например,
последовательность
-го члена
последовательности. Некоторая последовательность является решением данного рекуррентного соотношения,
если при подстановке этой последовательности соотношение тождественно выполняется. Например,
последовательность


 . Значит,
. Значит, 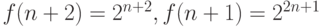 .
Но при любом
.
Но при любом  имеет место тождество
имеет место тождество 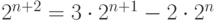 . Поэтому
. Поэтому  является решением
указанного соотношения.
является решением
указанного соотношения.Решение рекуррентного соотношения  -го порядка называется общим, если оно зависит от
-го порядка называется общим, если оно зависит от  произвольных постоянных
произвольных постоянных 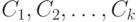 и путем подбора этих постоянных
можно получить любое решение данного соотношения. Например, для соотношения
и путем подбора этих постоянных
можно получить любое решение данного соотношения. Например, для соотношения
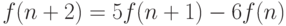 |
( 8.1) |
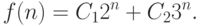 |
( 8.2) |
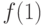 и
и  .
Поэтому нам надо доказать, что для любых чисел
.
Поэтому нам надо доказать, что для любых чисел  и
и  найдутся такие значения
найдутся такие значения 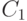 и
и 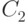 , что
, что
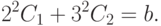
 и
и  система уравнений
система уравнений