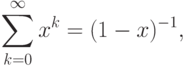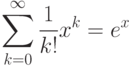Производящие функции
В комбинаторных задачах на подсчет числа объектов при наличии
некоторых ограничений искомым решением часто является последовательность 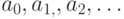 , где
, где 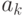 - число искомых
объектов "размерности"
- число искомых
объектов "размерности"  . Например, если мы ищем число
разбиений числа, то можем принять
. Например, если мы ищем число
разбиений числа, то можем принять 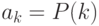 , если ищем число подмножеств
, если ищем число подмножеств  -элементного множества, то
-элементного множества, то  и т.д. В этом случае удобно
последовательности
и т.д. В этом случае удобно
последовательности 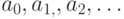 , поставить в соответствие
формальный ряд
, поставить в соответствие
формальный ряд
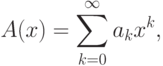 |
(
8.12)
|
называемый
производящей
функцией для данной последовательности.
Название
формальный
ряд для данной последовательности означает,
что (8.12) мы трактуем только как удобную
запись нашей последовательности
- в данном случае несущественно, для каких (действительных или
комплексных) значений переменной

он сходится. Поэтому мы
никогда не будем вычислять
значение такого ряда для конкретного значения переменной

, мы будем только выполнять некоторые
операции на таких рядах, а
затем определять
коэффициенты при отдельных степенях переменной

. Для
произвольных рядов
мы определим операцию сложения:
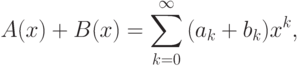 |
(
8.13)
|
операцию умножения на число (действительное или комплексное):
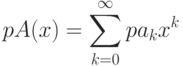 |
(
8.14)
|
и
произведение Коши
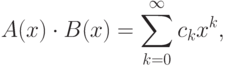 |
(
8.15)
|
где
 |
(
8.16)
|
Если
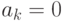
для
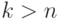
, то ряд (8.12) будем
отождествлять с многочленом
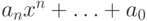
.
Из математического анализа известно, что если ряд (8.12) сходится в
некоторой окрестности нуля, то его сумма

является аналитической
функцией в этой окрестности и
 |
(
8.17)
|
(
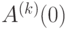
обозначает
значение 
-й производной
функции

для
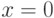
; ряд 8.12 - это не что иное, как ряд Маклорена функции

). Более того, когда
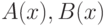
являются аналитическими функциями в
окрестности нуля, то формулы (8.13)-(8.16) будут справедливы, если
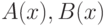
трактовать как значения функций

в
точке

, а ряды понимать в обычном смысле, т.е. так, как в математическом анализе. Это
сохраняющее
операции взаимно однозначное соответствие между рядами,
сходящимися в окрестности нуля, и функциями, аналитическими в окрестности
нуля, позволяет отождествить
формальный ряд (8.12) с определенной через
него аналитической функцией в случае рядов, сходящихся в окрестности нуля
(несмотря на то, что ряды мы будем трактовать всегда как формальные ряды,
то есть только как формальную
запись их коэффициентов). Таким образом,
будем писать, например,
и т.д.
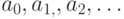 , где
, где 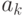 - число искомых
объектов "размерности"
- число искомых
объектов "размерности"  . Например, если мы ищем число
разбиений числа, то можем принять
. Например, если мы ищем число
разбиений числа, то можем принять 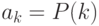 , если ищем число подмножеств
, если ищем число подмножеств  -элементного множества, то
-элементного множества, то  и т.д. В этом случае удобно
последовательности
и т.д. В этом случае удобно
последовательности 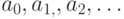 , поставить в соответствие
формальный ряд
, поставить в соответствие
формальный ряд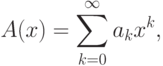
 он сходится. Поэтому мы
никогда не будем вычислять значение такого ряда для конкретного значения переменной
он сходится. Поэтому мы
никогда не будем вычислять значение такого ряда для конкретного значения переменной  , мы будем только выполнять некоторые операции на таких рядах, а
затем определять коэффициенты при отдельных степенях переменной
, мы будем только выполнять некоторые операции на таких рядах, а
затем определять коэффициенты при отдельных степенях переменной  . Для
произвольных рядов
. Для
произвольных рядов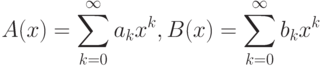
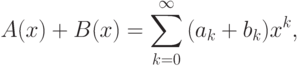
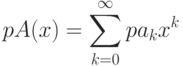
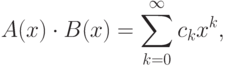

 для
для 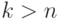 , то ряд (8.12) будем
отождествлять с многочленом
, то ряд (8.12) будем
отождествлять с многочленом 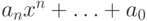 .
Из математического анализа известно, что если ряд (8.12) сходится в
некоторой окрестности нуля, то его сумма
.
Из математического анализа известно, что если ряд (8.12) сходится в
некоторой окрестности нуля, то его сумма  является аналитической
функцией в этой окрестности и
является аналитической
функцией в этой окрестности и
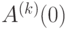 обозначает значение
обозначает значение  -й производной
функции
-й производной
функции  для
для 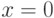 ; ряд 8.12 - это не что иное, как ряд Маклорена функции
; ряд 8.12 - это не что иное, как ряд Маклорена функции  ). Более того, когда
). Более того, когда 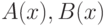 являются аналитическими функциями в
окрестности нуля, то формулы (8.13)-(8.16) будут справедливы, если
являются аналитическими функциями в
окрестности нуля, то формулы (8.13)-(8.16) будут справедливы, если 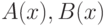 трактовать как значения функций
трактовать как значения функций  в
точке
в
точке  , а ряды понимать в обычном смысле, т.е. так, как в математическом анализе. Это
сохраняющее операции взаимно однозначное соответствие между рядами,
сходящимися в окрестности нуля, и функциями, аналитическими в окрестности
нуля, позволяет отождествить формальный ряд (8.12) с определенной через
него аналитической функцией в случае рядов, сходящихся в окрестности нуля
(несмотря на то, что ряды мы будем трактовать всегда как формальные ряды,
то есть только как формальную запись их коэффициентов). Таким образом,
будем писать, например,
, а ряды понимать в обычном смысле, т.е. так, как в математическом анализе. Это
сохраняющее операции взаимно однозначное соответствие между рядами,
сходящимися в окрестности нуля, и функциями, аналитическими в окрестности
нуля, позволяет отождествить формальный ряд (8.12) с определенной через
него аналитической функцией в случае рядов, сходящихся в окрестности нуля
(несмотря на то, что ряды мы будем трактовать всегда как формальные ряды,
то есть только как формальную запись их коэффициентов). Таким образом,
будем писать, например,