| Россия |
Целые и последовательности (последовательное распределение)
Различные способы представлений конечных последовательностей (или начальных сегментов бесконечных последовательностей) и операции над ними
Последовательное распределение. С вычислительной точки зрения простейшим представлением конечной последовательности является список ее членов, расположенных по порядку в последовательных ячейках памяти.
Так, 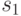 хранится, начиная с ячейки
хранится, начиная с ячейки 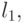
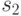 хранится, начиная с ячейки
хранится, начиная с ячейки 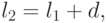
 хранится, начиная с ячейки
хранится, начиная с ячейки 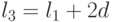 и так далее, где
и так далее, где 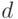 - число ячеек, требуемых для хранения одного элемента последовательности.
- число ячеек, требуемых для хранения одного элемента последовательности.
Описанное выше представление последовательности имеет ряд преимуществ.
Во-первых, оно легко осуществимо и требует небольших расходов в смысле памяти.
Кроме того, оно полезно и потому, что существует простое соотношение
между  и адресом ячейки, в которой хранится
и адресом ячейки, в которой хранится 
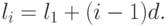
Например, чтобы представить массив размером 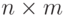
 |
( 2.4) |
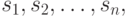 в которой каждое
в которой каждое 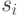 в свою очередь является последовательностью
из
в свою очередь является последовательностью
из  элементов
элементов  -й строки
нашей матрицы. Таким образом, число ячеек, требуемых для записи
элемента
-й строки
нашей матрицы. Таким образом, число ячеек, требуемых для записи
элемента 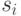 (будем обозначать это число символом
(будем обозначать это число символом  ),
равно
),
равно  где
где  - число
ячеек, требуемых для записи элемента
- число
ячеек, требуемых для записи элемента 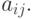 Поскольку
последовательность
Поскольку
последовательность 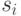 начинается в ячейке
начинается в ячейке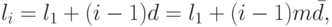
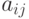 будет иметь следующий адрес:
будет иметь следующий адрес:![l_i + (j - 1)\bar d = l_1 +
[(i - 1)m + (j - 1)]\bar d.](/sites/default/files/tex_cache/74707572177cdd340acba6de9a6bb08c.png)
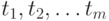 в которой каждое
в которой каждое 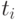 в свою очередь является последовательностью из элементов
в свою очередь является последовательностью из элементов  -го столбца матрицы.
-го столбца матрицы.Последовательное распределение, наряду с преимуществами, имеет
значительные недостатки. Например, такое представление становится неудобным,
если
требуется изменить последовательность путем включения новых и исключения
имеющихся там элементов. Включение между 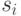 и
и 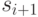 нового элемента
требует сдвига
нового элемента
требует сдвига 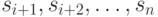 вправо на одну
позицию; аналогично,
исключение
вправо на одну
позицию; аналогично,
исключение 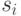 требует сдвига тех же элементов на одну позицию
влево. С точки
зрения времени обработки, такое передвижение элементов может оказаться
дорогостоящим, и в случае динамических последовательностей лучше использовать
технику связного распределения, рассматриваемую в следующей лекции.
требует сдвига тех же элементов на одну позицию
влево. С точки
зрения времени обработки, такое передвижение элементов может оказаться
дорогостоящим, и в случае динамических последовательностей лучше использовать
технику связного распределения, рассматриваемую в следующей лекции.
Характеристические
векторы. Важной разновидностью последовательного
распределения является случай, когда такому представлению подвергается
последовательность некоторой основной последовательности 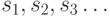 В этом случае можно представить последовательность более удобно,
используя характеристический
вектор - последовательность из нулей и единиц,
где
В этом случае можно представить последовательность более удобно,
используя характеристический
вектор - последовательность из нулей и единиц,
где  -й разряд равен единице, если
-й разряд равен единице, если 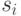 принадлежит
рассматриваемой последовательности, и нулю в противном случае.
принадлежит
рассматриваемой последовательности, и нулю в противном случае.
Например, характеристический вектор начального сегмента последовательности (2.3)
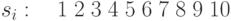
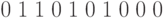
 , потребуется
, потребуется  слов.
Замечая далее, что для
слов.
Замечая далее, что для  число
число 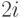 не простое,
можно сэкономить половину этого поля, выписывая разряды только для чисел видов
не простое,
можно сэкономить половину этого поля, выписывая разряды только для чисел видов 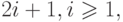 и запоминая, что простое число 2 отсутствует. Таким образом, простые числа, меньшие чем
и запоминая, что простое число 2 отсутствует. Таким образом, простые числа, меньшие чем 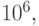 можно записать
только 15625 словами. Поскольку число простых чисел, меньших
можно записать
только 15625 словами. Поскольку число простых чисел, меньших 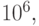 равно 78498, последовательное представление, описанное ранее, потребовало бы поля в пять раз меньшего размера.
равно 78498, последовательное представление, описанное ранее, потребовало бы поля в пять раз меньшего размера.Характеристические векторы полезны в ряде случаев. Их полезность вытекает
из их компактности, существования простого фиксированного соотношения
между  и адресом
и адресом  -го разряда и возможности при таком
представлении очень легко исключать элементы.
-го разряда и возможности при таком
представлении очень легко исключать элементы.
Главное неудобство характеристических векторов состоит в том, что они не
экономичны. Исключение составляют "плотные" последовательности
последовательностей 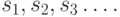 Кроме того, их трудно
использовать, если не существует простого соотношения между
Кроме того, их трудно
использовать, если не существует простого соотношения между  и
и 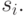 Если такое соотношение сложное, то использование характеристических векторов может быть очень не экономичным в смысле времени обработки. Если последовательности недостаточно
плотные, то значительным может оказаться объем памяти. В случае простых чисел
между
Если такое соотношение сложное, то использование характеристических векторов может быть очень не экономичным в смысле времени обработки. Если последовательности недостаточно
плотные, то значительным может оказаться объем памяти. В случае простых чисел
между  и
и 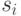 имеется простое соотношение:
имеется простое соотношение: 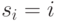 (или
(или 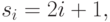 если использовать только нечетные числа). Теорема о простых числах утверждает, что число простых чисел, меньших
если использовать только нечетные числа). Теорема о простых числах утверждает, что число простых чисел, меньших 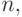 приблизительно равно
приблизительно равно 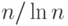 ; таким образом, простые числа относительно плотно распределены в множестве целых чисел.
; таким образом, простые числа относительно плотно распределены в множестве целых чисел.

