Бином Ньютона
Получим производящую функцию для конечной последовательности чисел 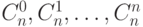 . Известно, что
. Известно, что
и
Эти равенства являются частными случаями более общей формулы, дающей
разложение для

. Запишем

в виде
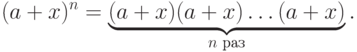 |
(
10.4)
|
Раскроем скобки в правой части этого равенства, причем будем записывать все
множители в том порядке, в котором они нам встретятся. Например,
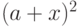
запишем в виде
 |
(
10.5)
|
а
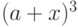
- в виде
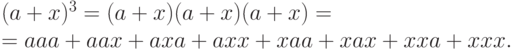 |
(
10.6)
|
Видно, что в формулу (10.5) входят все
размещения с повторениями,
составленные из букв

и

по две буквы в каждом
размещении, а в формулу (10.6) -
размещения с повторениями из тех же букв, но состоящие
из трех букв каждое. То же самое и в общем случае — после раскрытия скобок в
формуле (10.4) мы получим всевозможные
размещения с повторениями букв

и

, состоящие из

элементов. Приведем подобные
члены. Подобными будут члены, содержащие одинаковое количество букв

(тогда и букв

в них будет поровну). Найдем, сколько будет членов, в которые входит

букв

и, следовательно,
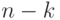
букв

. Эти
члены являются перестановками с повторениями, составленными из

букв

и
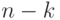
букв

. Поэтому их число равно
Отсюда вытекает, что после приведения подобных членов
выражение 
войдет с коэффициентом
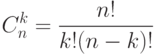
. Итак, мы доказали, что
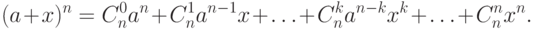 |
(
10.7)
|
(10.7) принято называть формулой бинома Ньютона. Если положить в этом
равенстве
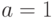
, то получим
 |
(
10.8)
|
Мы видим, что
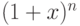
является производящей функцией для
чисел
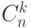
,

.
С помощью этой производящей функции можно сравнительно просто доказать
многие свойства чисел
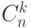
.
Ряд Ньютона
Мы назвали, как это обычно делают, формулу  биномом
Ньютона. Это наименование с точки зрения истории математики неверно.
Формулу для
биномом
Ньютона. Это наименование с точки зрения истории математики неверно.
Формулу для  хорошо знали среднеазиатские математики
Омар Хайям, Гиясэдди и другие. В
Западной Европе задолго до Ньютона она была известна Блэзу Паскалю. Заслуга же
Ньютона была в ином - ему удалось обобщить формулу
хорошо знали среднеазиатские математики
Омар Хайям, Гиясэдди и другие. В
Западной Европе задолго до Ньютона она была известна Блэзу Паскалю. Заслуга же
Ньютона была в ином - ему удалось обобщить формулу  на
случай нецелых показателей. Именно, он доказал, что если
на
случай нецелых показателей. Именно, он доказал, что если  -
положительное число и
-
положительное число и  , то для любого
действительного значения
, то для любого
действительного значения  имеет место равенство
имеет место равенство
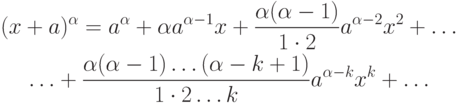 |
(
10.9)
|
Только теперь получилось не конечное число слагаемых, а бесконечный ряд. В
случае, когда

-
натуральное число,

обращается в нуль. Но эта скобка входит в коэффициент всех членов, начиная с
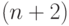
-го,
и потому все эти члены разложения равны нулю. Поэтому при натуральном

ряд (10.9) превращается в конечную сумму.
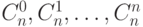 . Известно, что
. Известно, что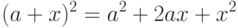

 . Запишем
. Запишем  в виде
в виде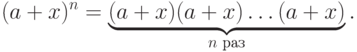
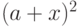 запишем в виде
запишем в виде
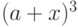 - в виде
- в виде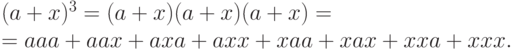
 и
и  по две буквы в каждом
размещении, а в формулу (10.6) - размещения с повторениями из тех же букв, но состоящие
из трех букв каждое. То же самое и в общем случае — после раскрытия скобок в
формуле (10.4) мы получим всевозможные размещения с повторениями букв
по две буквы в каждом
размещении, а в формулу (10.6) - размещения с повторениями из тех же букв, но состоящие
из трех букв каждое. То же самое и в общем случае — после раскрытия скобок в
формуле (10.4) мы получим всевозможные размещения с повторениями букв  и
и  , состоящие из
, состоящие из  элементов. Приведем подобные
члены. Подобными будут члены, содержащие одинаковое количество букв
элементов. Приведем подобные
члены. Подобными будут члены, содержащие одинаковое количество букв  (тогда и букв
(тогда и букв  в них будет поровну). Найдем, сколько будет членов, в которые входит
в них будет поровну). Найдем, сколько будет членов, в которые входит  букв
букв  и, следовательно,
и, следовательно, 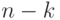 букв
букв  . Эти
члены являются перестановками с повторениями, составленными из
. Эти
члены являются перестановками с повторениями, составленными из  букв
букв  и
и 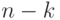 букв
букв  . Поэтому их число равно
. Поэтому их число равно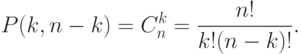
 войдет с коэффициентом
войдет с коэффициентом 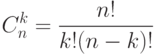 . Итак, мы доказали, что
. Итак, мы доказали, что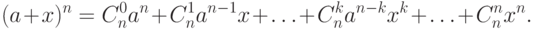
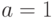 , то получим
, то получим
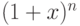 является производящей функцией для
чисел
является производящей функцией для
чисел 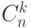 ,
,  .
С помощью этой производящей функции можно сравнительно просто доказать
многие свойства чисел
.
С помощью этой производящей функции можно сравнительно просто доказать
многие свойства чисел 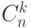 .
. биномом
Ньютона. Это наименование с точки зрения истории математики неверно.
Формулу для
биномом
Ньютона. Это наименование с точки зрения истории математики неверно.
Формулу для  хорошо знали среднеазиатские математики
Омар Хайям, Гиясэдди и другие. В
Западной Европе задолго до Ньютона она была известна Блэзу Паскалю. Заслуга же
Ньютона была в ином - ему удалось обобщить формулу
хорошо знали среднеазиатские математики
Омар Хайям, Гиясэдди и другие. В
Западной Европе задолго до Ньютона она была известна Блэзу Паскалю. Заслуга же
Ньютона была в ином - ему удалось обобщить формулу  на
случай нецелых показателей. Именно, он доказал, что если
на
случай нецелых показателей. Именно, он доказал, что если  -
положительное число и
-
положительное число и  , то для любого
действительного значения
, то для любого
действительного значения  имеет место равенство
имеет место равенство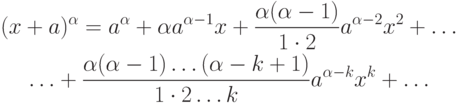
 - натуральное число,
- натуральное число,  обращается в нуль. Но эта скобка входит в коэффициент всех членов, начиная с
обращается в нуль. Но эта скобка входит в коэффициент всех членов, начиная с 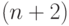 -го,
и потому все эти члены разложения равны нулю. Поэтому при натуральном
-го,
и потому все эти члены разложения равны нулю. Поэтому при натуральном  ряд (10.9) превращается в конечную сумму.
ряд (10.9) превращается в конечную сумму.