Классические и квантовые коды
Торические коды.
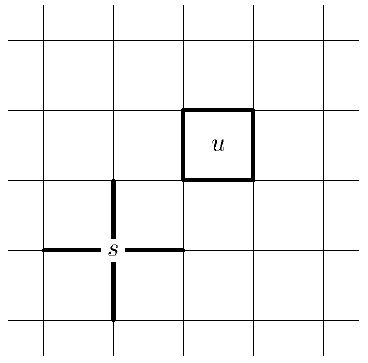
Приведем важный пример симплектического кода. Он строится так. Пусть есть квадратная решетка размера  на торе. Сопоставим каждому ее ребру по q-биту. Таким образом, всего имеется
на торе. Сопоставим каждому ее ребру по q-биту. Таким образом, всего имеется 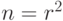 q-битов. Проверочные операторы будут двух типов.
q-битов. Проверочные операторы будут двух типов.
Тип I задается вершинами. Выберем некоторую вершину  и сопоставим ей проверочный оператор
и сопоставим ей проверочный оператор
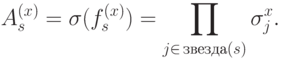
Тип II задается гранями. Выберем некоторую грань  и сопоставим ей проверочный оператор
и сопоставим ей проверочный оператор
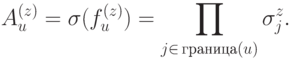
Операторы 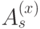 и
и 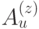 коммутируют, поскольку граница и звезда всегда пересекаются по четному числу ребер. (Перестановочность операторов одного типа очевидна.)
коммутируют, поскольку граница и звезда всегда пересекаются по четному числу ребер. (Перестановочность операторов одного типа очевидна.)
Хотя мы указали 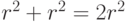 проверочных операторов (по одному на грань и на вершину), между ними есть соотношения. Произведение всех
проверочных операторов (по одному на грань и на вершину), между ними есть соотношения. Произведение всех 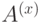 -операторов, как и произведение всех
-операторов, как и произведение всех 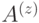 -операторов, равны тождественному. Можно показать, что других соотношений нет. Поэтому
-операторов, равны тождественному. Можно показать, что других соотношений нет. Поэтому 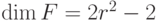 , а
, а 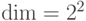 . Поэтому торический код позволяет закодировать два q-бита. Посмотрим, чему равно кодовое расстояние для торического кода.
. Поэтому торический код позволяет закодировать два q-бита. Посмотрим, чему равно кодовое расстояние для торического кода.
Для торического кода имеются естественные разложения

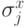 , либо только из
, либо только из 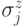 . Такие коды называются CSS кодами (по фамилиям авторов, впервые рассмотревших этот класс кодов [25, 44]). В случае торического кода элементы подпространств
. Такие коды называются CSS кодами (по фамилиям авторов, впервые рассмотревших этот класс кодов [25, 44]). В случае торического кода элементы подпространств 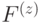 ,
, 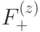 имеют вид
имеют вид 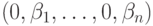 ; им можно сопоставить 1-цепи, т.е. формальные линейные комбинации ребер с коэффициентами
; им можно сопоставить 1-цепи, т.е. формальные линейные комбинации ребер с коэффициентами 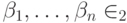 . Элементам подпространств
. Элементам подпространств 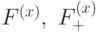 сопоставляются 1-коцепи. Рассмотрим вектор
сопоставляются 1-коцепи. Рассмотрим вектор  , отвечающий грани с номером
, отвечающий грани с номером  . Ему будет сопоставлена 1-цепь, являющаяся границей этой грани. Легко видеть, что пространство
. Ему будет сопоставлена 1-цепь, являющаяся границей этой грани. Легко видеть, что пространство 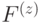 состоит из всех 1-границ. Аналогично, векторам
состоит из всех 1-границ. Аналогично, векторам 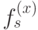 будут сопоставляться 1-кограницы, порождающие все пространство 1-кограниц.
будут сопоставляться 1-кограницы, порождающие все пространство 1-кограниц.Возьмем произвольный элемент 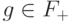 ,
, 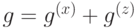 . Условия коммутирования запишутся следующим образом:
. Условия коммутирования запишутся следующим образом:

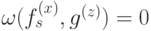 , нужно, чтобы в любой звезде было четное число ребер с ненулевыми весами из
, нужно, чтобы в любой звезде было четное число ребер с ненулевыми весами из 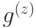 . Другими словами,
. Другими словами, 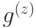 — это 1-цикл (с коэффициентами в
— это 1-цикл (с коэффициентами в  ). Аналогично,
). Аналогично, 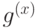 должен быть 1-коциклом.
должен быть 1-коциклом.Итак, пространства 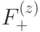 ,
, 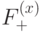 состоят из 1-циклов и 1-коциклов, а пространства
состоят из 1-циклов и 1-коциклов, а пространства 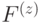 ,
, 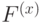 состоят из 1-границ и 1-кограниц. Следовательно, кодовое расстояние есть минимальная мощность (количество ненулевых коэффициентов) по циклам, не являющимся границами, и коциклам, не являющимся кограницами. Легко видеть, что этот минимум равен
состоят из 1-границ и 1-кограниц. Следовательно, кодовое расстояние есть минимальная мощность (количество ненулевых коэффициентов) по циклам, не являющимся границами, и коциклам, не являющимся кограницами. Легко видеть, что этот минимум равен  (нужны либо цикл, либо разрез, не гомологичные 0). Это означает, что торический код исправляет
(нужны либо цикл, либо разрез, не гомологичные 0). Это означает, что торический код исправляет 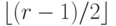 ошибок.
ошибок.
Будем обозначать коды описанного вида через  .
.
Замечание. Торические коды являются очень важным примером, обладающим рядом замечательных свойств. В частности, это коды с локальными проверками. Последовательность кодов называется кодами с локальными проверками, если выполнены следующие условия:
- каждый проверочный оператор действует на ограниченное константой число q-битов;
- каждый q-бит входит в ограниченное константой число проверочных операторов;
- кодовое расстояние неограниченно возрастает.
Такие коды представляют интерес для задачи построения вычислительных схем, устойчивых к ошибкам. При исправлении ошибок могут происходить новые ошибки. Но для кодов с локальными проверками схемы исправления ошибок имеют фиксированную глубину, поэтому одна ошибка при работе такой схемы портит ограниченное число q-битов.
Процедура исправления ошибок.
Определение 14.6 и теорема 14.2 указывают только на принципиальную возможность восстановить исходное состояние системы после действия ошибки. На примере симплектических кодов покажем, как реализовать процедуру исправления ошибки.
Рассмотрим частный случай, к которому все сводится. Пусть имеются две ошибки, заданные операторами  ,
, 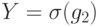 . Тогда
. Тогда 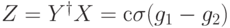 (
( 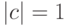 ). Назовем синдромом ошибки
). Назовем синдромом ошибки 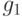 вектор
вектор 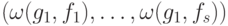 (для
(для  — аналогично).
— аналогично).
Возьмем вектор  . Обозначим
. Обозначим  . Проверочные операторы действуют на
. Проверочные операторы действуют на 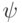 так:
так: 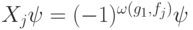 . Поэтому, измеряя собственные числа
. Поэтому, измеряя собственные числа  на состоянии
на состоянии 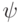 , можно измерить синдром.
, можно измерить синдром.
Если кодовое расстояние равно  , то выполнено
, то выполнено
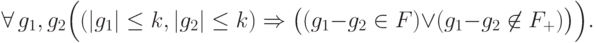
 означает эквивалентность ошибок
означает эквивалентность ошибок 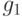 и
и  , т.е.
, т.е.  для любого вектора
для любого вектора 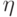 из кодового подпространства. Условие
из кодового подпространства. Условие  равносильно тому, что синдромы ошибок
равносильно тому, что синдромы ошибок 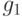 и
и  не совпадают. Итак, либо ошибки эквивалентны, либо их можно различить по синдрому. Следовательно, по синдрому можно определить ошибку с точностью до эквивалентности, т.е. по модулю подпространства
не совпадают. Итак, либо ошибки эквивалентны, либо их можно различить по синдрому. Следовательно, по синдрому можно определить ошибку с точностью до эквивалентности, т.е. по модулю подпространства  .
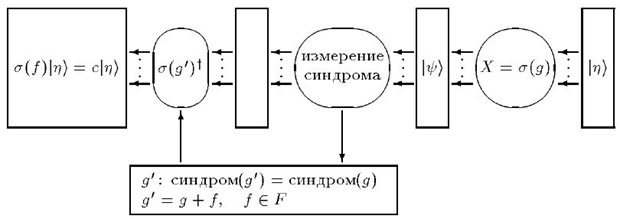
.Теперь ясно, как нужно исправлять ошибку. После того как определен синдром, применим оператор, обратный к оператору восстановленной по синдрому ошибки. Получим состояние, отличающееся от исходного лишь на фазовый множитель. Вся процедура изображена на рис. 14.2.
Выше рассмотрен случай ошибки типа 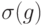 . На самом деле ошибка состоит в действии преобразования матриц плотности вида
. На самом деле ошибка состоит в действии преобразования матриц плотности вида
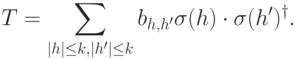
Задача 14.6. Постройте полиномиальный алгоритм определения ошибки по синдрому для торического кода.