НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 14: Классические и квантовые коды

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 15.03.2007 | Уровень: профессионал | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать программу

Модель независимых ошибок в квантовом случае.

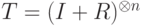Предположим, что на каждый q-бит действует одно и то же малое возмущение. Это означает, что на матрицу плотности рассматриваемой системы из q-битов действует преобразование $T=(I+R)^{\otimes n}$ , где — "мало". В классическом случае малое возмущение означает малую вероятность ошибки. В квантовом случае малое возмущение меняет матрицы плотности "не слишком сильно". Чтобы придать этому выражению точный смысл, нужно ввести норму на матрицах плотности, характеризующую их близость, а затем — такую норму на преобразованиях матриц плотности, чтобы выполнялось условие: малое по норме преобразование переводит матрицу плотности в близкую к ней.

Начнем с того, что выясним, какие нормы пригодны для характеризации близости матриц плотности. Матрица плотности, как мы помним из "Квантовые вероятности" , задает вероятностное распределение на чистых состояниях. 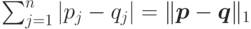Вероятностные распределения естественно сравнивать в $\ell^1$ -норме: если $\boldsymbol p=(p_1,\dots,p_n)$ , $\boldsymbol q=(q_1,\dots,q_n)$ — два распределения, то мерой их различия считаем $\sum_{j=1}^{n}|p_j-q_j|=\|\boldsymbol p-\boldsymbol q\|_1$ . Дадим определение аналогичной нормы для матриц плотности.

Определение 14.4. Следовая норма оператора $A\in\LL(\calN)$ равна

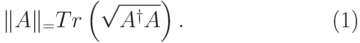$\begin{equation}\label{след} \|A\|_\trr=Tr\left(\sqrt{A^\dagger A}\right). \end{equation}$

( 14.3)

Для эрмитова оператора следовая норма — это сумма модулей собственных чисел.

Задача 14.1. Проверьте, что (14.3) действительно определяет норму. Докажите, что

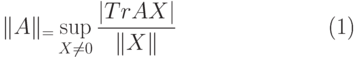$\begin{equation}\label{trace-norm-sup-def} \|A\|_\trr=\sup\limits_{X\ne0}\frac{|Tr AX|}{\|X\|} \end{equation}$

( 14.4)

( $\|X\|$ — операторная норма, см. опр. 7.2).

Задача 14.2. Проверьте выполнение следующих свойств следовой нормы:

$\|AB\|_\trr\leq\|B\|\: \|A\|_\trr$ ,
$\|BA\|_\trr\leq\|B\|\: \|A\|_\trr$ ,
$|Tr A|\leq\|A\|_\trr$ ,
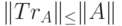$\|Tr_\calM A\|_\trr\leq\|A\|_\trr$ ,
$\|A\otimes B\|_\trr=\|A\|_\trr \|B\|_\trr$ .

Следующая лемма показывает, почему можно рассматривать следовую норму для матриц плотности как аналог $\ell^1$ -нормы для вероятностных распределений.

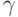
Лемма 14.2. Пусть $\calN=\bigoplus_{j}\calN_j$ — разложение пространства $\calN$ в прямую сумму взаимно ортогональных подпространств. Тогда для любой пары матриц плотности $\rho$ , $\gamma$

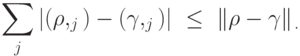
$\sum_{j} |\PP(\rho,\calN_j)-\PP(\gamma,\calN_j)|\ \le\ \|\rho-\gamma\|_\trr\hskip2pt.$

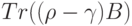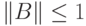Доказательство. Левую часть этого неравенства можно представить в виде $Tr((\rho-\gamma)B)$ , где $B=\sum_{j}(\pm\Pi_{\calN_j})$ . Ясно, что $\|B\|\le 1$ . Теперь применим представление следовой нормы в виде (14.4).

Теперь кажется естественным определить норму преобразования матриц плотности аналогично операторной норме

$\begin{equation}\label{Tsup1} \|T\|_1=\sup_{X\ne0}\frac{\|TX\|_\trr}{\|X\|_\trr} \end{equation}$

( 14.5)

и мерить этой нормой малость возмущения. Однако использование нормы (14.5) оказывается неудобным, так как она не согласована с тензорным произведением. Поясним это подробнее. Чтобы иметь оценку, аналогичную оценке (14.2) в классическом случае, мы должны написать разложение

$\begin{equation}\label{разложение-тензорной-степени} T=\left(I+R\right)^{\otimes n}=I+\sum_{|A|\le k}^{} R^{\otimes A}\otimes I_{[n]\setminus A}+ \underbrace{\sum\limits_{|A|>k}^{} R^{\otimes A}\otimes I_{[n]\setminus A}}_{P} \end{equation}$

( 14.6)

и оценить норму

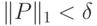при условии $\|P\|_1<\delta$ . Если бы выполнялось неравенство 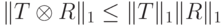$\|T\otimes R\|_1\leq \|T\|_1\|R\|_1$ , можно было бы буквально повторить оценку (14.2). Однако это неравенство не всегда выполняется.

Пример 14.3. Рассмотрим преобразование

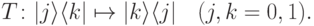
$T\colon |j\rangle\langle k|\mapsto|k\rangle\langle j|\quad (j,k=0,1).$

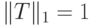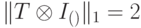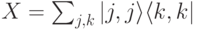Очевидно, что $\|T\|_1=1$ , однако $\|T\otimes I_{\LL(\BB)}\|_1=2$ . (Подействуйте преобразованием $T\otimes I_{\LL(\BB)}$ на оператор $X=\sum_{j,k}|j,j\rangle\langle k,k|$ .)

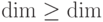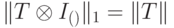Оказывается (ниже это будет доказано), что патология примера 14.3 имеет ограничение по размерности. А именно, если $\dim\calG\geq\dim\calN$ , то $\|T\otimes I_{\LL(\calG)}\|_1=\|T\|_\trn$ , где величина 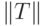$\|T\|_\trn$ от $\calG$ не зависит. Прежде чем доказывать это утверждение, посмотрим на его следствия.

Во-первых, ясно, что определенная таким образом величина 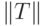$\|T\|_\trn$ является нормой.

Во-вторых, поскольку следовая норма мультипликативна относительно тензорного умножения, то $\|T\otimes R\|_1\geq\|T\|_1\|R\|_1$ . Поэтому $\|T\|_\trn\geq\|T\|_1$ .

В-третьих, из определения следует, что 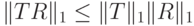$\|TR\|_1\leq\|T\|_1\|R\|_1$ , поэтому имеем такие неравенства

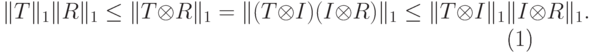$\begin{equation}\label{tensor-inequalities} \|T\|_1\|R\|_1\leq\|T\otimes R\|_1=\|(T\otimes I)(I\otimes R)\|_1\leq \|T\otimes I\|_1\|I\otimes R\|_1. \end{equation}$

( 14.7)

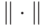Из этих неравенств следует мультипликативность нормы $\|\cdot\|_\trn$ относительно тензорного умножения.

Чтобы доказать приведенное выше свойство норм $\|T\otimes I\|_1$ , дадим другое определение величины $\|T\|_\trn$ .

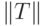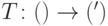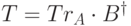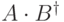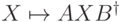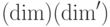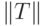Определение 14.5. Рассмотрим представления $T\colon \LL(\calN)\to\LL(\calN')$ в виде $T=Tr_\calF A\cdot B^\dagger$ . Здесь $A\cdot B^\dagger$ обозначает преобразование $X\mapsto AXB^\dagger$ , а $A,B\in\LL(\calN,\calN'\otimes\calF)$ , где $\calF$ — произвольное унитарное пространство размерности не меньшей, чем $(\dim\calN)(\dim\calN')$ . Тогда $\|T\|_\trn$ — точная нижняя грань чисел вида $\|A\|\:\|B\|$ (это операторные нормы) по всем представлениям указанного вида.

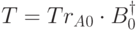Замечание. Условие $\dim\calF\ge(\dim\calN)(\dim\calN')$ гарантирует, что существует хотя бы одно представление $T=Tr_\calF A_0\cdot B_0^\dagger$ . Для минимизации произведения $\|A\|\:\|B\|$ достаточно рассматривать операторы с нормами $\|A\|\le\|A_0\|$ и $\|B\|\le\|B_0\|$ , поэтому инфимум достигается в силу компактности. То, что он не зависит от размерности $\calF$ , вытекает из следующей теоремы.

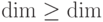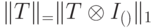Теорема 14.1. Если $\dim\calG\geq\dim\calN$ , то $\|T\|_\trn=\|T\otimes I_{\LL(\calG)}\|_1$ .

Доказательство. Пусть $TX=Tr_\calF AXB^\dagger$ . Тогда, используя свойства следовой нормы из задачи 14.2, получаем

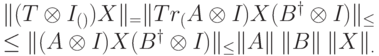
$\begin{equation*} \|(T\otimes I_{\LL(\calG)})X\|_\trr= &\|Tr_\calF(A\otimes I_{\calG})X(B^\dagger\otimes I_{\calG})\|_\trr\leq\\ \leq& \|(A\otimes I_{\calG})X(B^\dagger\otimes I_{\calG})\|_\trr\leq \|A\|\:\|B\|\:\|X\|_\trr. \end{equation*}$

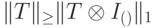Поэтому $\|T\|_\trn\geq\|T\otimes I_{\LL(\calG)}\|_1$ .

Доказать неравенство в обратную сторону несколько сложнее. Без уменьшения общности, $\|T\|_\trn=1$ . Инфимум в определении 14.5 достигается при $\|A\|=\|B\|=1$ .

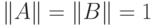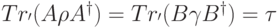Покажем сначала, что существуют три матрицы плотности $\rho,\gamma\double\in\LL(\calN)$ и $\tau\in\LL(\calF)$ , такие что $Tr_{\calN'}(A\rho A^\dagger)=Tr_{\calN'}(B\gamma B^\dagger)=\tau$ . Пусть

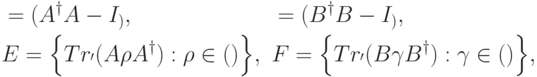
$\begin{align*} &\calK=\Ker(A^\dagger A-I_\calN), &&\calL=\Ker(B^\dagger B-I_\calN),\\ &E=\Bigl\{ Tr_{\calN'}(A\rho A^\dagger):\rho\in\DD(\calK) \Bigr\}, && F=\Bigl\{ Tr_{\calN'}(B\gamma B^\dagger):\gamma\in\DD(\calL) \Bigr\}, \end{align*}$

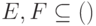где $\DD(\calL)$ обозначает множество матриц плотности на пространстве $\calL$ . Тогда $E,F\subseteq\DD(\calF)$ , поэтому в качестве 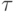$\tau$ годится любой элемент из $E\cap F$ .

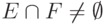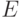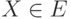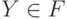Докажем, что $E\cap F\not=\emptyset$ . Так как и — компактные выпуклые множества, достаточно доказать, что не существует разделяющей их гиперплоскости. Другими словами, нет такого эрмитова оператора $Z\in\LL(\calF)$ , что Tr XZ>Tr YZ для любых $X\in E$ , $Y\in F$ . А это, в свою очередь, следует из минимальности величины $\|A\|\,\|B\|$ по отношению к преобразованию

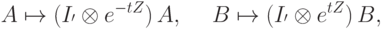
$A\mapsto(I_{\calN'}\otimes e^{-tZ})\,A,\quad\ B\mapsto(I_{\calN'}\otimes e^{tZ})\,B,$

где

положительно, но мало.

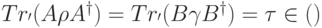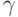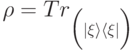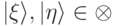Итак, пусть $Tr_{\calN'}(A\rho A^\dagger)=Tr_{\calN'}(B\gamma B^\dagger)=\tau \in\DD(\calF)$ , где $\rho,\gamma\double\in\DD(\calN)$ . Представим $\rho$ и $\gamma$ в виде $\rho=Tr_\calG\Bigl(|\xi\rangle\langle\xi|\Bigr)$ , $\gamma=Tr_\calG\Bigl(|\eta\rangle\langle\eta|\Bigr)$ , где $|\xi\rangle,|\eta\rangle\in\calN\otimes\calG$ — единичные векторы. Здесь мы используем условие 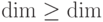$\dim\calG\geq\dim\calN$ и утверждение 9.1. Положим 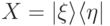$X=|\xi\rangle\langle\eta|$ . 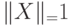Очевидно, что $\|X\|_\trr=1$ .

Докажем, что 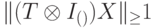$\|(T\otimes I_{\LL(\calG)})X\|_\trr\geq 1$ . Обозначим

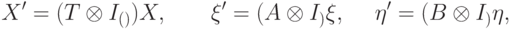
$X'=(T\otimes I_{\LL(\calG)})X, \qquad \ket{\xi'}=(A\otimes I_\calG)\ket\xi, \quad\ \ket{\eta'}=(B\otimes I_\calG)\ket\eta,$

тогда

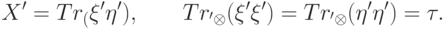
$X'=Tr_\calF(\ket{\xi'}\bra{\eta'}),\qquad Tr_{\calN'\otimes\calG}(\ket{\xi'}\bra{\xi'})= Tr_{\calN'\otimes\calG}(\ket{\eta'}\bra{\eta'})=\tau.$

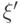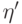Отсюда, во-первых, следует, что векторы $\ket{\xi'}$ и $\ket{\eta'}$ имеют единичную длину. Во-вторых, найдется унитарный оператор

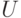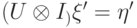на пространстве $\calN'\otimes\calG$ , такой что $(U\otimes I_\calF)\ket{\xi'}=\ket{\eta'}$ (это утверждение из задачи 9.3). Следовательно,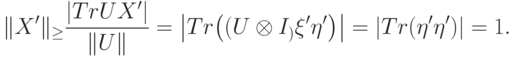

$\|X'\|_\trr\ge \frac{|Tr UX'|}{\|U\|} = \left| Tr\big((U\otimes I_\calF)\ket{\xi'}\bra{\eta'}\big) \right| = \left| Tr(\ket{\eta'}\bra{\eta'}) \right|=1.$

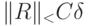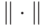Теперь можно оценить остаточный член в формуле (14.6), почти дословно повторяя рассуждения в классическом случае. Если $\|R\|_1<\delta$ , то $\|R\|_\trn<C\delta$ , где — константа (все нормы эквивалентны, причем множитель ограничен размерностью пространства; действует на пространстве матриц плотности одного q-бита). Используя мультипликативность нормы $\|\cdot\|_\trn$ , заключаем, что

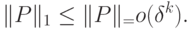
$\|P\|_1\leq\|P\|_\trn=o(\delta^k).$

Поэтому будем пренебрегать всеми слагаемыми из

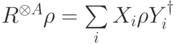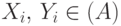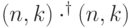, а действие всех остальных слагаемых будем учитывать. Преобразования $R^{\otimes A}$ имеют вид $R^{\otimes A}\rho=\sum\limits_{i}^{} X_i\rho Y_i^\dagger$ , где $X_i,\, Y_i\in \calE(A)$ ; символически это можно записать так: $R^{\otimes A}\in \calE(A)\cdot\calE^\dagger(A)$ . Сумма преобразований $\sum_{|A|\le k}^{} R_1^{\otimes A}\otimes I_{[n]\setminus A}$ лежит в $\calE(n,k)\cdot\calE^\dagger(n,k)$ . Таким образом, мы приходим к выводу, что нужно рассматривать ошибки из $\calE(n,k)$ .

Дальше >>

Классические и квантовые вычисления

Классические и квантовые вычисления

Классические и квантовые коды

Модель независимых ошибок в квантовом случае.

Вопросы и ответы

Студенты

Авторизоваться

Классические и квантовые вычисления

Классические и квантовые вычисления

Классические и квантовые коды

Модель независимых ошибок в квантовом случае.

Вопросы и ответы

Студенты