Базисные средства манипулирования реляционными данными: алгебра A Дейта и Дарвена

Избыточность Алгебры A

В формальной математической логике стандартным базисом для выражения всех возможных булевских функций является набор {NOT, AND, OR} (отрицание, дизъюнкция и конъюнкция). Известно, что этот набор традиционен, но избыточен, поскольку верны тождества 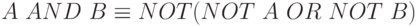и . (Эти тождества легко проверяются по таблицам истинности операций.) Оказывается (и это тоже легко проверить, опираясь на определения операций), что аналогичные тождества справедливы для операций <NOT>, <AND> и <OR> Алгебры A. Тем самым, в наборе базовых операций Алгебры A можно оставить операции <AND> и <NOT> (или <OR> и <NOT> ).

Реляционные аналоги штриха Шеффера и стрелки Пирса

Более того, в алгебре логики существуют две операции, через каждую из которых выражаются все три "базовые" операции: "штрих Шеффера" – – и "стрелка Пирса" – .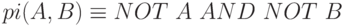

Легко видеть, что

• ;
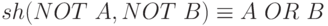• и
• .

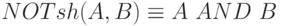Аналогично,

• ;
• и
• .

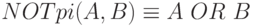Снова нетрудно проверить, что аналогичные тождества справедливы для реляционных вариантов штриха Шеффера 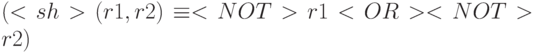и стрелки Пирса .

Поэтому можно свести набор операций Алгебры A к трем операциям: <sh> (или <pi> ), <RENAME> и <REMOVE>.

Избыточность операции переименования

Наконец, покажем, что избыточна и операция <RENAME>. Для иллюстрации снова воспользуемся отношением СЛУЖАЩИЕ из рис. 4.14. Пусть нам нужен результат операции СЛУЖАЩИЕ <RENAME> (ПРО_НОМ, НОМЕР_ПРОЕКТА) (мы по-прежнему предполагаем, что множество значений домена атрибута ПРО_НОМ ограничено значениями, представленными в теле отношения СЛУЖАЩИЕ ). Возьмем бинарное отношение ПРО_НОМ_НОМЕР_ПРОЕКТА (рис. 4.15), где каждый из кортежей содержит два одинаковых значения номера проекта и в тело отношения входят все значения домена атрибута ПРО_НОМ^{8Это "константное" отношение, тело которого не зависит от текущего содержания тела отношения СЛУЖАЩИЕ.} . Тогда, как показано на рис. 4.15, вычисление выражения (СЛУЖАЩИЕ <AND> ПРО_НОМ_НОМЕР_ПРОЕКТА) <REMOVE> (ПРО_НОМ) приводит к желаемому результату.

Рис. 4.15. Избыточность операции <RENAME>

Тем самым, можно сократить набор операций Алгебры A до двух операций: <sh> (или <pi>) и <REMOVE>^{9И конечно, в Алгебре A, как и в алгебре Кодда, должна присутствовать операция присваивания переменной отношения.} .

Заключение

Базисом Алгебры A являются операции реляционного отрицания (дополнения), реляционной конъюнкции (или дизъюнкции ) и проекции ( удаления атрибута ). Реляционные аналоги логических операций определяются в терминах отношений на основе обычных теоретико-множественных операций и позволяют выражать напрямую операции пересечения, декартова произведения, естественного соединения и объединения отношений. Путем комбинирования базовых операций выражаются операции переименования атрибутов, соединения общего вида, взятия разности отношений. Алгебра A позволяет лучше осознать логические основы реляционной модели, хотя, безусловно, является в меньшей степени ориентированной на практическое применение, чем алгебра Кодда.

Как нам кажется, в методическом отношении Алгебра A важна, прежде всего, тем, что в ней реляционная операция естественного соединения является одной из базовых операций, в отличие от алгебры Кодда, где эта операция имела второстепенное значение. Это важно по той причине, что, как мы увидим в лекции 7, операция естественного соединения играет первостепенную роль в классическом подходе к проектированию реляционных баз данных на основе нормализации.