Базисные средства манипулирования реляционными данными: алгебра A Дейта и Дарвена

Полнота Алгебры A

Покажем, что Алгебра A является полной, т. е. на основе введенных операций выражаются все операции алгебры Кодда, рассмотренной в предыдущей лекции.

К настоящему моменту в состав базовых операций Алгебры A входят операция <REMOVE> в качестве аналога операции PROJECT, а также операция переименования атрибутов <RENAME>. UNION является частным случаем операции <OR>, TIMES, INTERSECT и NATURAL JOIN – частные случаи операции <AND>. Нам осталось показать, что через операции Алгебры A выражаются операции взятия разности MINUS, ограничения ( WHERE ), соединения общего вида ( JOIN ) и реляционного деления ( DIVIDE BY ).

Выводимость операции взятия разности

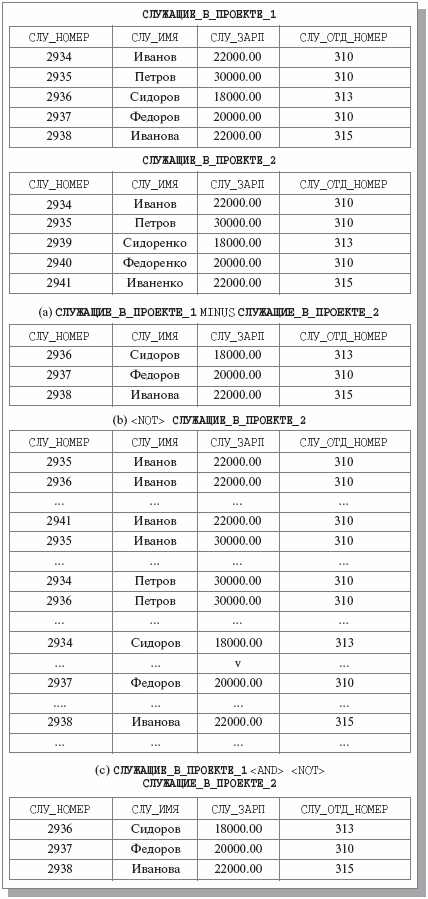
Покажем, что операция MINUS выражается через другие операции Алгебры A. Для наглядности снова воспользуемся отношениями СЛУЖАЩИЕ_В_ПРОЕКТЕ_1 и СЛУЖАЩИЕ_В_ПРОЕКТЕ_2 c рис. 4.3 (для удобства повторим его в верхней части рис. 4.7). Для простоты (хотя это несущественно) будем предполагать, что множества значений доменов, на которых определены атрибуты СЛУ_НОМЕР, СЛУ_ИМЯ, СЛУ_ЗАРП и СЛУ_ОТД_НОМЕР, ограничены значениями, содержащимися в телах отношений. Также для удобства покажем результат операции СЛУЖАЩИЕ_В_ПРОЕКТЕ_1 MINUS СЛУЖАЩИЕ_В_ПРОЕКТЕ_2 на рис. 4.7a. Заметим, что тело результата содержит все кортежи первого операнда, кроме кортежей Иванова и Петрова, поскольку они входят и в тело второго операнда.

Рис. 4.7. Выразимость операции MINUS через операции <NOT> и <AND>

Посмотрим теперь, что является телом результата операции <NOT> СЛУЖАЩИЕ_В_ПРОЕКТЕ_2 (рис. 4.7b). В него входят все кортежи, соответствующие схеме отношения СЛУЖАЩИЕ_В_ПРОЕКТЕ_2 (и схеме отношения СЛУЖАЩИЕ_В_ПРОЕКТЕ_1 ), которые не входят в тело отношения СЛУЖАЩИЕ_В_ПРОЕКТЕ_2. В том числе в тело результата этой операции входят и кортежи Сидорова, Федорова и Ивановой из тела отношения СЛУЖАЩИЕ_В_ПРОЕКТЕ_1.

Тогда очевидно, что результат операции СЛУЖАЩИЕ_В_ПРОЕКТЕ_1 <AND> <NOT> СЛУЖАЩИЕ_В_ПРОЕКТЕ_2 (пересечение тела первого операнда с телом результата операции <NOT> ) является в точности тем же, что и результат операции СЛУЖАЩИЕ_В_ПРОЕКТЕ_1 MINUS СЛУЖАЩИЕ_В_ПРОЕКТЕ_2 (рис. 4.7c).

В общем случае нетрудно доказать, что если отношения r1 и r2 совместимы по объединению, то r1 MINUS r2 = r1 <AND> <NOT> r2.