|
Хотелось бы иметь возможность читать текст сносок при использовании режима "Версия для печати" |
Базисные средства манипулирования реляционными данными: алгебра A Дейта и Дарвена
Соединения общего вида
При наличии того факта, что операция взятия расширенного декартова произведения TIMES является частным случаем операции <AND>, после того как мы научились с помощью Алгебры A выполнять ограничения, становится очевидно, что через операции Алгебры A выражаются и соединения общего вида. В общем случае, чтобы получить результат соединения общего вида произвольных отношений A и B, нужно:
- выполнить над одним из отношений одну или несколько операций <RENAME>, чтобы избавиться от общих имен атрибутов;
- выполнить над полученными отношениями операцию <AND>, производящую расширенное декартово произведение ;
- и для полученного отношения выполнить одну или несколько операций <AND> с отношениями-константами, чтобы должным образом ограничить его.
Реляционное деление
Пусть имеются отношения r1{A, B} и r2{B}. Утверждается, что результат r1 DIVIDE BY r2 совпадает с результатом выражения (r1 PROJECT A) MINUS (((r2 TIMES (r1 PROJECT A)) MINUS r1) PROJECT A) в терминах операций реляционной алгебры Кодда или (r1 <REMOVE> B) <AND> <NOT> (((r2 <AND> (r1 <REMOVE> B)) <AND> <NOT> r1) <REMOVE> B) в терминах операций Алгебры A.
Действительно, результатом выполнения операции r1 PROJECT A является унарное отношение со схемой {A}, кортежи тела которого содержат все значения атрибута A из тела отношения r1. Результат выражения r2 TIMES (r1 PROJECT A) – это бинарное отношение со схемой {A, B}, в тело которого входят все возможные комбинации значений атрибута B в теле отношения r2 и атрибута A в теле отношения r1. В теле результата вычисления выражения (r2 TIMES (r1 PROJECT A)) MINUS r1 останутся только те кортежи, которые не входят во второй операнд, т. е. кортежи с таким значением атрибута A, что значение атрибута B, принадлежащее телу r2, не является значением атрибута B ни в одном кортеже тела отношения r1. Следовательно, если мы возьмем проекцию результата выражения (r2 TIMES (r1 PROJECT A)) MINUS r1 на атрибут A, то в результирующем унарном отношении останутся только те значения A, которые не должны попасть в результат операции r1 DIVIDE BY r2. После выполнения завершающей операции MINUS мы получим желаемый результат.
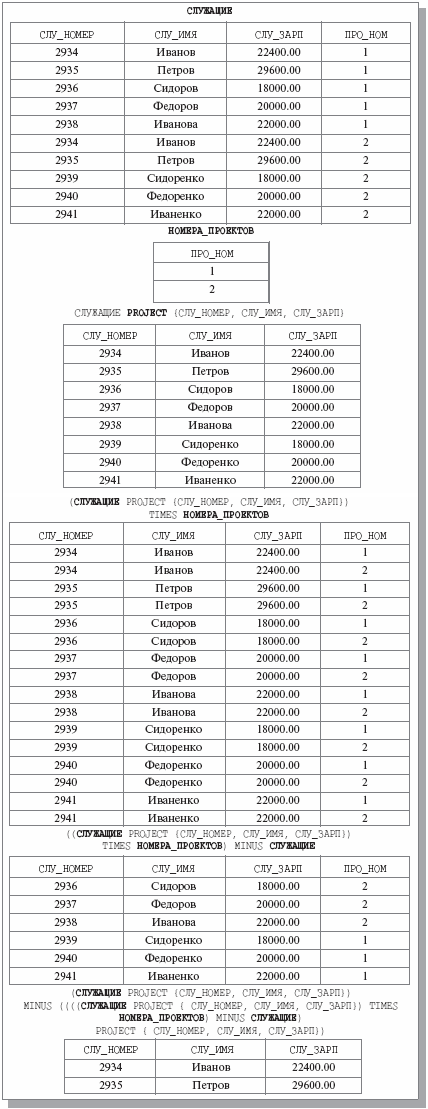
Для иллюстрации воспользуемся отношениями СЛУЖАЩИЕ и НОМЕРА_ПРОЕКТОВ, которые мы уже применяли в предыдущих примерах. Для удобства мы воспроизводим их на рис. 4.14. На этом же рисунке показаны промежуточные и окончательный результаты вычисления выражения (СЛУЖАЩИЕ PROJECT {СЛУ_НОМЕР, СЛУ_ИМЯ, СЛУ_ЗАРП}) MINUS ((((СЛУЖАЩИЕ PROJECT {СЛУ_НОМЕР, СЛУ_ИМЯ, СЛУ_ЗАРП}) TIMES НОМЕРА_ПРОЕКТОВ) MINUS СЛУЖАЩИЕ) PROJECT {СЛУ_НОМЕР, СЛУ_ИМЯ, СЛУ_ЗАРП}).
Тем самым, мы показали, что пяти операций Алгебры A достаточно для выражения всех операций алгебры Кодда из лекции 3. Но на самом деле число операций можно еще более сократить, что мы и продемонстрируем в следующем разделе.