Типовые ошибки разработки тестовых заданий
Рассмотрим некоторые типовые ошибки составления тестовых заданий на основе тестовых заданий по информатике и новым информационным технологиям.
Они аналогичны (с точки зрения тестологии) ошибкам и в других предметных областях.
Обозначим здесь и ниже тестовое задание с ошибками (тестологии) через T–, ошибки – через О, а откорректированный тест – через Т+.
Т–. Каждый символ при кодировании кодируется одним байтом. Слово "Тестирование" в ЭВМ обычно кодируется комбинацией длины: а) 12 бит. б) 72 бит. в) 96 бит. г) 192 бит.
О. Наличие двух предложений. Неясно, следует ли включать кавычки (как символы) в длину слова. Нестрогое слово "обычно" недопустимо.
T+. "Тестирование" (без кавычек) кодируется по принципу "1 символ – 1 байт" битовой комбинацией длины: а) 12. б) 72. в) 96. г) 192.
Возможен вариант: T+. Слово "Тестирование" (без кавычек) кодируется в ASCII комбинацией длины: а) 12. б) 72. в) 96. г) 192.
Часто формулируют и так: слово Тестирование кодируется по принципу "символ – байт" комбинацией длины… а) 12. б) 72. в) 96. г) 192.
Последний вариант нам кажется менее удачным, как с позиции грамматики русского языка, так и с позиции информатики (пояснения принципа кодировки).
Обратим здесь внимание на необходимость слова "длины". Если убрать это слово, то ответ всегда – 2 бита: любое слово всегда кодируется комбинацией из двух бит (0 и 1).
Каждое слово в тесте – значащее. Лишних слов также не должно быть.
T–. Задуманное число до 500 можно отгадать односложными вопросами, задав их не более: а) 500. б) 50. в) 10. г) 9.
О. Условие не завершено функционально. Понятие "односложное" с точки зрения правил русского языка не требует дополнительного уточнения, но с точки зрения проверяемых знаний и умений (а это принцип бинарного поиска) – предпочтительно пояснить и уточнить.
T+. Задуманное натуральное число до 500 можно отгадать бинарным поиском, задав вопросов не более: а) 500. б) 50. в) 10. г) 9.
T–. Решение системы уравнений:  будет удовлетворять условию: а)
будет удовлетворять условию: а) 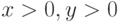 . б)
. б) 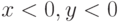 . в)
. в)  . г)
. г) 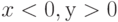 .
.
О. Ошибки преобразования единиц измерения сообщений или решения системы уравнений, допущенные на любом этапе решения, не всегда приводят к неправильному ответу. Задание не информативно. Неясна, например, причина и не видны некоторые следствия допущенных ошибок.
Т+. Решение системы уравнений:  имеет вид: а)
имеет вид: а) 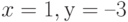 . б)
. б)  . в)
. в) 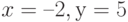 . г)
. г)  . Этот тест рассчитан на знание не только единиц измерения сообщений, но и на умение их преобразовывать друг к другу, а на "заключительном участке" – на умение решать системы показательных уравнений. Ошибки, допущенные на любом из этих этапов – существенны и информативны.
. Этот тест рассчитан на знание не только единиц измерения сообщений, но и на умение их преобразовывать друг к другу, а на "заключительном участке" – на умение решать системы показательных уравнений. Ошибки, допущенные на любом из этих этапов – существенны и информативны.
Т–. Если рассматривается нижеследующий фрагмент таблицы истинности некоторой функции 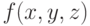
то из приведённых ниже функции 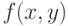 , этой искомой функции может соответствовать только функция, указанная в пункте: а)
, этой искомой функции может соответствовать только функция, указанная в пункте: а) 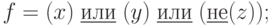 б)
б) 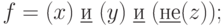 в)
в) 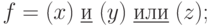 г)
г)  .
.
О. Многословие, излишние слова, особенно это нежелательно в сочетание с таблицами, графиками и т.д.
T+. Фрагменту таблицы истинности вида:
из приведенных ниже логических функции f(x,y,z) может соответствовать только функция: а) 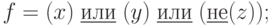 б)
б)  в)
в) 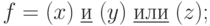 г)
г)  .
.
Существенны слова "из приведенных ниже". Без них тест некорректен, допуская множество других функций, отличных от приведенных.
T–. Список основных устройств ввода-вывода персонального компьютера: процессор, сканер, дисплей, диск, плоттер, принтер, мышь, трекбол, клавиатура, регистр, содержит различных устройств ввода информации: а)1. б)3. в)4. г)5.
О. Много ключевых слов задания: "список", "основные", "устройства", "персональный компьютер", "ввод", "вывод", "информация".
T+. Список {сканер, дисплей, диск, плоттер, принтер, мышь, трекбол, клавиатура} содержит устройств ввода: а) 1. б) 3. в) 4. г) 5.
T–. Основные функции операционной системы: а) управление данными к обрабатываемым ЭВМ программам. б) управление программами. в) управление ресурсами.
О. Ответы – не одинаковой длины. Мало дистракторов. Слово "управление" нужно вынести в формулировку задания.
T+. Полный набор основных функций ОС – это управление: а) данными. б) программами. в) ресурсами. г) данными, программами и ресурсами.
Впрочем, нужно стараться избегать ответов типа г).
T–. Фрагмент:  вычисляет значение
вычисляет значение  равное: а) 10. б) 32. в) 31. г) 63.
равное: а) 10. б) 32. в) 31. г) 63.
О. Правильный ответ легко вычисляется и стоит первым в списке неупорядоченных по возрастанию или убыванию вариантов ответов.
T+. Фрагмент:  вычислит
вычислит  равное: а) 63. б) 32. в) 31. г) 10.
равное: а) 63. б) 32. в) 31. г) 10.
T–. В синтаксической конструкции: 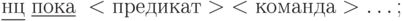 пропущено ключевое слово: а)
пропущено ключевое слово: а) 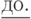 б)
б) 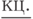 в)
в) 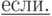 г)
г) 
О. Наличие в условии задания  подсказывает правильный ответ, даже если не понимется смысл этого ключевого слова и смысл самой конструкции, на что и направлено тестовое задание.
подсказывает правильный ответ, даже если не понимется смысл этого ключевого слова и смысл самой конструкции, на что и направлено тестовое задание.
T+. В синтаксической конструкции:  пропущено ключевое слово: а)
пропущено ключевое слово: а) 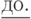 б)
б)  в)
в) 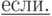 г)
г) 
Здесь уже необходимо знание синтаксиса (и даже семантики) правильной конструкции.
T–. Графические файлы могут иметь все расширения, указанные в списке: а)*.rtf; *.bmp; *.bas. б) *.tif; *.exe; *.bmp. в) *.jpg; *.bmp; *.tif. г) *.rtf; *.bmp; *.tif; *.jpg.
О. В вариантах а), б) присутствуют достаточно широко известные всем (в том числе и тем, кто не знает расширений графических файлов) расширения *.bas, *.exe. Кроме того, ответ г) – длиннее. Эти ответы – менее привлекательны.
T+. Графические файлы могут иметь все типы расширений, указанные в списке: а)*.rtf; *.bmp; *.com. б) *.tif; *.zip; *.bmp. в) *.jpg; *.bmp; *.tif. г) *.rtf; *.bmp; *.jpg.
Форма задания Т+ без звездочек также возможна.
T–. Последовательное выполнение команд ШАЯ:  даст значение
даст значение  , равное: а) 24. б) 10. в) 9. г) 6.
, равное: а) 24. б) 10. в) 9. г) 6.
О. Сокращение ШАЯ (школьный алгоритмический язык) – не вполне общепринятое и общеупотребительное, общеизвестное.
T+. Последовательное выполнение команд  школьного учебного алгоритмического языка даст значение
школьного учебного алгоритмического языка даст значение  , равное: а) 24. б) 10. в) 9. г) 6.
, равное: а) 24. б) 10. в) 9. г) 6.
При этом корректно следующее тестовое задание.
Т+. Windows - это: а) ОС. б) ППП. в) БД. г) СУБД.
T–. Значение выражения 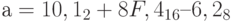 в десятичной системе равно: а) 139,25. б) 139,5. в) 138,5. г) 140,5. д) 143,25. е) 147.
в десятичной системе равно: а) 139,25. б) 139,5. в) 138,5. г) 140,5. д) 143,25. е) 147.
О. Много дистракторов. Последние дистракторы не рассчитаны на типовые ошибки, но остальные расчитаны на те или иные типовые ошибки. Поэтому последние два дистрактора можно "безболезненно" убрать.
T+. Значение выражения 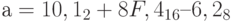 в десятичной системе равно: а) 138,5. б) 139,25. в) 139,5. г) 140,5.
в десятичной системе равно: а) 138,5. б) 139,25. в) 139,5. г) 140,5.
Заметим, что все эти дистракторы предполагают те или иные типовые ошибки перевода.
T–. Для предиката  , где
, где ![X=[1;30]](/sites/default/files/tex_cache/6e17a052d985b72f3caefc6028ac6b88.png) область истинности равна: а)
область истинности равна: а) 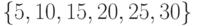 . б)
. б)  . в)
. в) 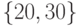 . г)
. г) 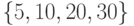 .
.
