Типовые ошибки разработки тестовых заданий
О. Для нецелых  из указанного множества допустимых значений предикат не определен (не определено понятие делимости нацело для нецелых чисел).
из указанного множества допустимых значений предикат не определен (не определено понятие делимости нацело для нецелых чисел).
T+. Для предиката  , заданного на множестве
, заданного на множестве 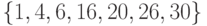 , область истинности - множество: а)
, область истинности - множество: а) 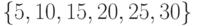 . б)
. б)  . в)
. в) 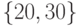 . г)
. г) 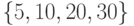 .
.
Возможно использование вместо  выражения
выражения 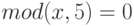 , но нужно учесть, что в этом случае цель задания (спецификация) изменяется, – проверяется еще и знание функции mod. Отметим, что в этом задании допускается неодинаковая длина дистракторов.
, но нужно учесть, что в этом случае цель задания (спецификация) изменяется, – проверяется еще и знание функции mod. Отметим, что в этом задании допускается неодинаковая длина дистракторов.
Другой пример ("вроде бы правильный").
Т–. Истинное значение при 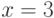 принимает предикат: а) "для каждого натурального
принимает предикат: а) "для каждого натурального  существует
существует  ". б) "натуральное
". б) "натуральное  – четно, если
– четно, если 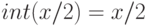 ". в) "произведение
". в) "произведение 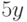 - нечетно". г) "натуральное
- нечетно". г) "натуральное  – нечетно, если
– нечетно, если 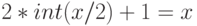 ".
".
О. На первый взгляд, - все вроде правильно. Проведём тщательный анализ. При подстановке значения 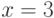 дистрактор а) становится неопределенным (не высказывание): "для каждого 3 существует
дистрактор а) становится неопределенным (не высказывание): "для каждого 3 существует 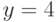 "! Дистрактор б) некорректно сравнивает два различных по типу выражения – целое
"! Дистрактор б) некорректно сравнивает два различных по типу выражения – целое 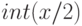 и вещественное
и вещественное 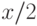 (при любом натуральном х значение
(при любом натуральном х значение 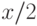 – вещественное). Дистрактор в) – "слегка некорректен": "произведение 15 – нечетно" (неясно произведение каких чисел). Если бы было сформулировано в виде "произведение
– вещественное). Дистрактор в) – "слегка некорректен": "произведение 15 – нечетно" (неясно произведение каких чисел). Если бы было сформулировано в виде "произведение  - нечетно", то тогда выражение превратилось бы истинное высказывание: "произведение 5*3 – нечётно".
- нечетно", то тогда выражение превратилось бы истинное высказывание: "произведение 5*3 – нечётно".
Т+. Предикатом с переменной  является высказывательная форма: а) "для каждого натурального
является высказывательная форма: а) "для каждого натурального  существует
существует  "; б) "натуральное
"; б) "натуральное  – четно, если
– четно, если 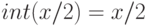 ". в) "произведение
". в) "произведение 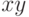 при целых
при целых 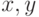 - нечетно". г) "натуральное
- нечетно". г) "натуральное  – нечетно, если
– нечетно, если 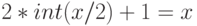 ".
".
Здесь в правильном ответе г) сравниваются однотипные выражения, в отличие от б).
Этот пример (точнее, его откорректированный вариант Т+) можно отнести к группе С. Он показывает несостоятельность негласно существующего мнения, что задания группы С в тестовой форме невозможны, нельзя использовать, хуже и т.д. Для выбора ответа к приведенному заданию, как мы видим, понадобились достаточно глубокие знания (на что и направлена группа С).
T–. Значение выражения  равно: а) 1. б) 2. в)
равно: а) 1. б) 2. в)  . г) 6.
. г) 6.
О. Типовыми ошибками при вычислении этого выражения будут (ранжируем по экспериментально или экспертно устанавливаемой частоте их встречаемости и важности): 1) 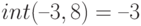 (нет полных знаний о математической функции "антье" или
(нет полных знаний о математической функции "антье" или ![[x]](/sites/default/files/tex_cache/3e5314e9fd31509fdeb83faa0f729ba2.png) ,
, 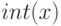 ); 2)
); 2) 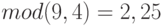 ("путают целочисленное и обычное деление"), 3)
("путают целочисленное и обычное деление"), 3) 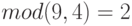 ("путают
("путают  и
и 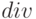 "). На эти ошибки и должны быть "нацелены" дистракторы. Итак, мы решили вначале "обратные" задачи. Для перечисленных типовых ошибок получаем неправильные варианты ответов: 1) –2; 2) –1,75; 3) –0,75 (комбинация 1) и 2)). Их и нужно предусмотреть в вариантах ответов.
"). На эти ошибки и должны быть "нацелены" дистракторы. Итак, мы решили вначале "обратные" задачи. Для перечисленных типовых ошибок получаем неправильные варианты ответов: 1) –2; 2) –1,75; 3) –0,75 (комбинация 1) и 2)). Их и нужно предусмотреть в вариантах ответов.
T+. Значение выражения  равно: а) –3. б) –2. в) –1,75. г) –0,75.
равно: а) –3. б) –2. в) –1,75. г) –0,75.
T–. Фрагмент:  вычислит значение
вычислит значение  равное цифре: а) единиц натурального числа
равное цифре: а) единиц натурального числа  . б) самого старшего разряда числа
. б) самого старшего разряда числа  . в)
. в)  -го разряда (начиная со старшего разряда) числа
-го разряда (начиная со старшего разряда) числа  . г)
. г)  -го разряда (начиная с младшего разряда) числа
-го разряда (начиная с младшего разряда) числа  .
.
О. Для допустимого значения 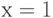 дистракторы а), б), в) также становятся правильными ответами. Кроме того, возможны такие входные
дистракторы а), б), в) также становятся правильными ответами. Кроме того, возможны такие входные  , при которых дистракторы могут дать правильные числовые ответы, например, при
, при которых дистракторы могут дать правильные числовые ответы, например, при 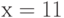 .
.
T+. Фрагмент: 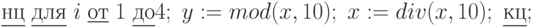 вычислит для
вычислит для 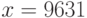 значение
значение  равное цифре: а) единиц числа
равное цифре: а) единиц числа  . б) десятков числа
. б) десятков числа  . в) сотен числа
. в) сотен числа  . г) тысяч числа
. г) тысяч числа  .
.
T–. Пусть в тесте приведены два задания. Задание 1. Выражение 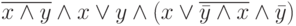 эквивалентно выражению: а) 1. б)
эквивалентно выражению: а) 1. б) 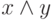 . в)
. в) 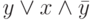 . г)
. г)  . Задание 2. После упрощения выражения
. Задание 2. После упрощения выражения 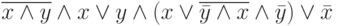 получим выражение: а) 1. б)
получим выражение: а) 1. б) 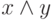 . в)
. в) 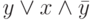 .. г)
.. г)  .
.
О. В результате правильного решения первого задания получим ответ г). Ясно, что ответ на второе задание равен 1, и он легко получается из ответа на первое задание. По крайней мере, если первое задание можно отнести к группе  (с натяжкой), то второе вкупе с первым, – только к группе
(с натяжкой), то второе вкупе с первым, – только к группе  (также с натяжкой), так как ориентирован на проверку знания лишь одной простой аксиомы:
(также с натяжкой), так как ориентирован на проверку знания лишь одной простой аксиомы: 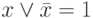 . Нарушена валидность (тестовое задание на проверку одной указанной аксиомы, как правило, - не нужно). Для сокращения времени составления задания и увеличения банка тестовых заданий, часто делают такие "добавки" к раннее придуманным корректным выражениям. Это очень вредный подход. В принципе, он допустим для формирования различных однотипных вариантов тестовых заданий. Не более.
. Нарушена валидность (тестовое задание на проверку одной указанной аксиомы, как правило, - не нужно). Для сокращения времени составления задания и увеличения банка тестовых заданий, часто делают такие "добавки" к раннее придуманным корректным выражениям. Это очень вредный подход. В принципе, он допустим для формирования различных однотипных вариантов тестовых заданий. Не более.
T+. В тесте могут быть приведены, например, два следующих задания. Задание 1. Выражение 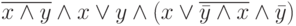 эквивалентно выражению: а) 1. б)
эквивалентно выражению: а) 1. б) 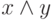 . в)
. в) 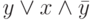 .. г)
.. г)  . Задание 2. Выражение
. Задание 2. Выражение  равносильно выражению: а)
равносильно выражению: а) 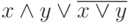 . б)
. б) 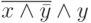 . в)
. в) 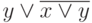 . г) 1.
. г) 1.
Рассмотрим примеры преобразования заданий в задания закрытой формы.
Т+. Термин "информатика" образован соединением слова "информация" и слова…
Т–. Частное от деления десятичного числа 12 на десятичное число 7 имеет меньшую относительную погрешность в представлении: а) 1,71 (десятичное). б) 1,55 (восьмеричное). в) 1,1011 (двоичное). г) 1,В5 (шестнадцатеричное).
О. Гетерогенность (информатика + математика, знание абсолютной и относительной погрешности из математики и систем счисления из информатики) в этом задании не является "жизненно необходимой". Задание лучше переформулировать так, как приведено ниже.
T+. Частное от деления десятичного числа 12 на десятичное число 7 точнее представлено числом: а) 1,71 (десятичное). б) 1,55 (восьмеричное). в) 1,1011 (двоичное). г) 1,В5 (шестнадцатеричное).
Понятие "точнее" здесь уже ясно хотя бы на интуитивном уровне и этого вполне достаточно для ответа (тем тестируемым, кто знает, что деление не всегда осуществимо точно, а это также входит в проверяемые заданием знания, умения и навыки).
T–. Число различных символов в закодированном по КОИ-8 сообщении вида 1111000111010000111100011001111011010000 равно: а) 6. б) 5. в) 4. г) 3.
О. Здесь, несомненно, у тестируемого возникнет вопрос: что такое КОИ-8? Не "спасёт" и употребление вместо КОИ-8 более известного стандарта ASCII. Лучше это тестовое задание переформулировать следующим образом.
T+. Различных символов в закодированном по принципу "1 символ – 1 байт" сообщении вида 1111000111010000111100011001111011010000: а) 6. б) 5. в) 4. г) 3.
Т+. В десятичном числе из  десятков и
десятков и  единиц, количество информации: а) в цифре десятков и цифре единиц – одинаково. б) в цифре десятков больше, чем в цифре единиц. в) в цифре единиц больше, чем в цифре десятков. г) в цифрах разрядов нельзя сравнивать, так как цифры неизвестны.
единиц, количество информации: а) в цифре десятков и цифре единиц – одинаково. б) в цифре десятков больше, чем в цифре единиц. в) в цифре единиц больше, чем в цифре десятков. г) в цифрах разрядов нельзя сравнивать, так как цифры неизвестны.
Такие тестовые задания можно вполне включать в олимпиадное задание, например, городского уровня или же в ЕГЭ (не требует знаний и умений, выходящих за рамки школьной программы).

