Анализ и обоснование тестирования
Случайная величина – числовая переменная (числовая функция), определённая на выборочном пространстве (или приписываемая некоторому выборочному пространству) таким образом, что каждой точке выборочного пространства соответствует одно и только одно значение этой переменной.
Если множество всех теоретически возможных значений величины  конечно или счётно, то её называют дискретной случайной величиной .
конечно или счётно, то её называют дискретной случайной величиной .
Функция  , которая для каждого возможного значения
, которая для каждого возможного значения 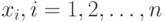 (или
(или 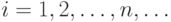 ) дискретной случайной величины
) дискретной случайной величины  равна вероятности
равна вероятности 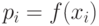 появления этого значения, задаёт распределение вероятностей случайной величины. Таким образом, эта функция задаёт множество значений, которые может принимать случайная величина, вместе с соответствующими им вероятностями.
появления этого значения, задаёт распределение вероятностей случайной величины. Таким образом, эта функция задаёт множество значений, которые может принимать случайная величина, вместе с соответствующими им вероятностями.
Величину 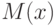 , определяемую формулой
, определяемую формулой
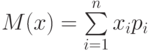 ,
,
называют математическим ожиданием дискретной случайной величины  .
.
Величину, определяемую формулой
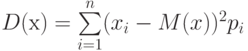 ,
,
называют дисперсией этой случайной величины.
Математическое ожидание характеризует центр распределения (аналог среднего выборки), а дисперсия – степень рассеяния значений случайной величины вокруг центра (аналог рассеяния в выборке). Эти формулы дают возможность получить оценку математического ожидания и дисперсии на основе опытных данных.
Если случайная величина распределена непрерывно и задана некоторой функцией распределения  , то
, то 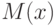 и
и 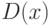 определяются по соответствующим формулам (для ограниченного и бесконечного множества изменения случайной величины):
определяются по соответствующим формулам (для ограниченного и бесконечного множества изменения случайной величины):
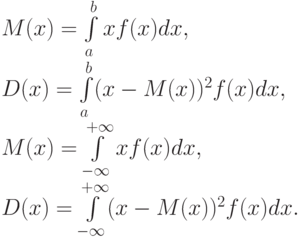
Основная цель статистических расчетов, как правило, состоит в том, чтобы по характеристикам выборки получить достоверную информацию о свойствах исходных генеральных совокупностей.
Рассмотрим теперь укрупнено (не приводя, как выше, алгоритмы на уровне, достаточном для реализации, программирования) комплекс задач, который связан с обоснованием принятия гипотез тестирования.
Есть процедуры, позволяющие отвергнуть проверяемую гипотезу как противоречащую имеющимся данным, либо убедиться в том, что гипотеза этим данным не противоречит.
Располагая каким-то распределением данных тестирования, можно исследовать возможность описания этой совокупности каким-то типовым распределением, если тип распределения неизвестен, а затем найти неизвестный параметр распределения, а также эффективность описания.
Наиболее часто рассматриваются гипотезы, в основе которых лежат известные распределения: нормальное (Гаусса), 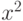 , Стьюдента и Фишера. Существуют различные процедуры проверки гипотезы о принадлежности заданного эмпирического распределения к некоторому теоретическому типу.
, Стьюдента и Фишера. Существуют различные процедуры проверки гипотезы о принадлежности заданного эмпирического распределения к некоторому теоретическому типу.
Рассмотрим нормальное распределение (распределение Гаусса).
Это распределение – наиболее часто встречающееся непрерывное распределение (точнее было бы сказать, что это распределение, к которому "подгоняется" большинство изучаемых распределений). Такому закону или его различным модификациям подчиняются многие наборы случайных величин. Общий вид нормального распределения задаётся функцией:
![f(x)=\frac{1}{\sqrt{2\pi D(x)}}exp\left[ -\frac{(x-M(x))^2}{2D(x)}\right]](/sites/default/files/tex_cache/9e4b8b3444769e8923c424ec2b6ac87f.png) .
.
Часто используется стандартное нормальное распределение или распределение вероятностей нахождения (попадания) случайной величины в интервал 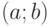 . Для вычисления значений такой функции используется интеграл (таблица значений этого, не берущегося в квадратурах, интеграла):
. Для вычисления значений такой функции используется интеграл (таблица значений этого, не берущегося в квадратурах, интеграла):
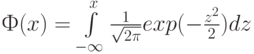 .
.
Необходимо на основе имеющихся результатов тестирования проверить гипотезу нормального распределения результатов тестирования, например, достижений (можно в качестве достижения принять среднее арифметическое по всем тестам) тестированных в зависимости от выборки.
Самый простой, но математически менее надежный алгоритм – построения графика (эскиза) и его анализ.
Процедура может быть следующей.
- Эти данные
 могут быть изображены графически, что даёт наглядное представление о центре их распределения и изменчивости. Для этого по оси абсцисс откладывают в порядке возрастания значения
могут быть изображены графически, что даёт наглядное представление о центре их распределения и изменчивости. Для этого по оси абсцисс откладывают в порядке возрастания значения 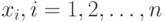 , а по оси ординат – частоты, т.е. количества случаев получения одинаковых показателей (или изменяющихся в определённых пределах).
, а по оси ординат – частоты, т.е. количества случаев получения одинаковых показателей (или изменяющихся в определённых пределах). - Соединяя построенные точки линиями, получаем диаграмму распределения. Для многих систем и процессов, при большом числе испытаний, диаграмма распределения близка к нормальной кривой распределения симметричной формы. Эта кривая имеет "колоколообразный" вид.
- Построив диаграмму распределения и заметив его схожесть с этой кривой, можно обосновать справедливость нормального распределения для ряда.
- Конец алгоритма.
Оценку соответствия рассматриваемого распределения нормальному распределению можно осуществить также и по величине асимметрии:
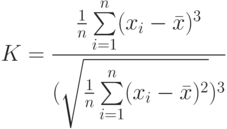
Если имеет место левая асимметрия (сдвиг влево), то это говорит о том, что в тесте были облегченные задания, на которые сумели правильно ответить подавляющее большинство испытуемых, а также были усложненные задания, с которыми не смогли справиться подавляющее большинство испытуемых.
Если имеет место правая асимметрия (сдвиг вправо), то это говорит о том, что в тесте был очень низкий порог трудности для данного контингента испытуемых.
Алгоритм проверки гипотезы о нормальном законе распределения с помощью коэффициента асимметрии может реализовываться следующими шагами.
- Вычислить среднее арифметическое
 .
. - Вычислить коэффициент асимметрии
 по вышеприведенной формуле.
по вышеприведенной формуле. - Так как для нормальной кривой распределения характерна симметричность относительно среднего значения, то значение
 , равное или достаточно близкое к нулю свидетельствует о симметричности распределения; чем больше значение
, равное или достаточно близкое к нулю свидетельствует о симметричности распределения; чем больше значение  , тем больше отклоняется наиболее часто встречающаяся в распределении величина от средней (больше смещена ось симметрии, больше асимметрия кривой), а сдвиг "колоколообразной" части кривой влево или вправо свидетельствует о чрезмерной легкости или сложности заданий.
, тем больше отклоняется наиболее часто встречающаяся в распределении величина от средней (больше смещена ось симметрии, больше асимметрия кривой), а сдвиг "колоколообразной" части кривой влево или вправо свидетельствует о чрезмерной легкости или сложности заданий. - Конец алгоритма.
Знание закона распределения баллов необходимо для выработки нормативной шкалы, которая позволит соотнести равные отрезки под кривой распределения равным количествам правильных ответов.
Распределение можно получить следующей процедурой:
- Сгенерировать случайную выборку тестируемых (из генеральной совокупности).
- Протестировать выборку и получить первичные баллы.
- Оценить баллами каждого испытуемого по отношению к баллам других участников.
- Найти число интервалов, на которые делится числовая прямая оценок и границы интервалов (например, для четырёхбалльной системы оценок квартили). Обычно находят балл некоторого испытуемого как процентную долю испытуемых, первичный балл которых ниже первичного балла данного испытуемого. Если распределение подчиняется нормальному закону, то интерквантильная широта равна
 , где
, где  – среднеквадратичное отклонение; если же распределение не подчиняется нормальному закону, то либо изменяют тесты до тех пор пока не получим нормальное распределение, либо принудительно нормализуют распределение, либо используют шкалы, ориентированные на другие типы распределений.
– среднеквадратичное отклонение; если же распределение не подчиняется нормальному закону, то либо изменяют тесты до тех пор пока не получим нормальное распределение, либо принудительно нормализуют распределение, либо используют шкалы, ориентированные на другие типы распределений.
Необходимо искусственно приводить распределение первичных тестовых оценок к нормальному виду, так как она наиболее изучена (проста) в математической статистике и дает возможность описывать диагностические нормы в компактной форме. Обычно рассматриваются гистограммы распределения первичных тестовых оценок. Они позволяют выявлять лево- и правостороннюю асимметрию, положительный или отрицательный эксцесс и другие "ненормальности". Применение известных статистических программных пакетов позволяет автоматизировать подгонку требуемого преобразования первичных тестовых оценок к комбинациям различных базисных аналитических функций, что также позволяет стандартизировать тестовые оценки.
