|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Редуцированные базисы решетки. Редуцирование базиса в решетке
20.4. ПРЕДЛОЖЕНИЕ. Пусть  - решетка с базисом
- решетка с базисом  и
предположим, что задано положительное число
и
предположим, что задано положительное число  , такое, что
для любого
вектора
, такое, что
для любого
вектора 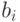 из исходного базиса решетки выполняется неравенство
из исходного базиса решетки выполняется неравенство  . Тогда алгоритм построения редуцированного базиса, описанный выше, требует для своего выполнения
. Тогда алгоритм построения редуцированного базиса, описанный выше, требует для своего выполнения  арифметических
операций над
целыми числами, двоичная длина которых представляет
арифметических
операций над
целыми числами, двоичная длина которых представляет  . Таким
образом, для построения редуцированного базиса достаточно
. Таким
образом, для построения редуцированного базиса достаточно  бинарных операций.
бинарных операций.
ДОКАЗАТЕЛЬСТВО.
Перед началом работы алгоритма величины  , определенные
формулами (20.12) удовлетворяют неравенству
, определенные
формулами (20.12) удовлетворяют неравенству  , что
легко следует из
упражнения 20.2. Таким образом,
перед началом работы алгоритма
, что
легко следует из
упражнения 20.2. Таким образом,
перед началом работы алгоритма  . Из определения
. Из определения  легко следует, что в
случае, когда
легко следует, что в
случае, когда  ,
,  - неотрицательное целое число,
которое не может обратиться в
нуль, в силу линейной независимости векторов, составляющих базис решетки.
Таким образом,
- неотрицательное целое число,
которое не может обратиться в
нуль, в силу линейной независимости векторов, составляющих базис решетки.
Таким образом,  во все время работы алгоритма. Выше
отмечалось, что при
перестановках элементов базиса, выполняемых алгоритмом построения
редуцированного базиса, величина
во все время работы алгоритма. Выше
отмечалось, что при
перестановках элементов базиса, выполняемых алгоритмом построения
редуцированного базиса, величина  убывает не медленнее
геометрической
прогрессии со знаменателем 3/4, следовательно, таких перестановок
выполняется
убывает не медленнее
геометрической
прогрессии со знаменателем 3/4, следовательно, таких перестановок
выполняется  . Мы оценили, таким образом,
сколько раз
в головной программе, в цикле "пока" встречается ситуация "то" в
условии
"если". Из доказательства конечности времени работы алгоритма следует,
что
ситуация "иначе" встречается также
. Мы оценили, таким образом,
сколько раз
в головной программе, в цикле "пока" встречается ситуация "то" в
условии
"если". Из доказательства конечности времени работы алгоритма следует,
что
ситуация "иначе" встречается также  раз. Итак,
тело цикла в
основном алгоритме выполняется
раз. Итак,
тело цикла в
основном алгоритме выполняется  раз. Внутренний цикл
в ситуации
"иначе" дает еще один множитель
раз. Внутренний цикл
в ситуации
"иначе" дает еще один множитель  для алгоритма A35, который выполняется
таким образом
для алгоритма A35, который выполняется
таким образом  раз. Переходим теперь к оценке
сложности
отдельных предписаний алгоритма A33.
раз. Переходим теперь к оценке
сложности
отдельных предписаний алгоритма A33.
В предписании "начальная-установка" два вложенных цикла дают 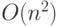 повторений тела цикла, в котором встречаются векторные операции: скалярное
произведение векторов, умножение вектора на число, вычитание векторов, что
дает еще один множитель
повторений тела цикла, в котором встречаются векторные операции: скалярное
произведение векторов, умножение вектора на число, вычитание векторов, что
дает еще один множитель  . При этом арифметические операции
выполняются над
рациональными числами. Сложность выполнения операций над этими числами оценим
несколько позже.
. При этом арифметические операции
выполняются над
рациональными числами. Сложность выполнения операций над этими числами оценим
несколько позже.
Количество арифметических операций в алгоритме A35, как легко видеть, равно  , такое же количество операций в алгоритме A36. Сравнивая количество
проходов через отдельные ветви алгоритма, получаем, что количество
арифметических операций в алгоритме представляется величиной
, такое же количество операций в алгоритме A36. Сравнивая количество
проходов через отдельные ветви алгоритма, получаем, что количество
арифметических операций в алгоритме представляется величиной  ,
что и утверждалось в первой части предложения.
,
что и утверждалось в первой части предложения.
Оценим теперь сложность выполнения арифметических операций, выполняемых
над
рациональными числами в процессе работы алгоритма A33. Прежде всего, опишем
множество значений, которые могут принимать знаменатели всех встречающихся во
время вычислений рациональных чисел. Покажем, что в качестве
знаменателей всех встречающихся чисел могут быть использованы только числа  , вычисляемые по формулам (20.12), а именно:
, вычисляемые по формулам (20.12), а именно:
 |
( 20.13) |
 |
( 20.14) |
 |
( 20.15) |
Первое из этих соотношений следует из упражнения 20.2.
Для доказательства второго соотношения выразим векторы 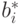 с
неопределенными коэффициентами
с
неопределенными коэффициентами  через исходный базис:
через исходный базис:

Неизвестные коэффициенты с фиксированным первым индексом  определяются из
системы линейных уравнений
определяются из
системы линейных уравнений
 |
( 20.16) |
Решая систему (20.16) методом Крамера, воспользовавшись формулой
(20.12) получаем,
что  для всех допустимых значений индексов.
Отсюда уже
вытекает соотношение (20.14).
для всех допустимых значений индексов.
Отсюда уже
вытекает соотношение (20.14).
Воспользовавшись соотношениями (19.2), (20.13) и (20.14), получаем цепочку равенств

Посмотрим теперь, как меняются величины  в процессе работы
алгоритма. В
начале работы алгоритма они вычисляются по формулам (20.12). В процессе
работы
эти величины меняются только при перестановке элементов базиса (в алгоритме A36 ). В этом случае
в процессе работы
алгоритма. В
начале работы алгоритма они вычисляются по формулам (20.12). В процессе
работы
эти величины меняются только при перестановке элементов базиса (в алгоритме A36 ). В этом случае  заменяется (в
обозначениях (20.1)-(20.5)) на
заменяется (в
обозначениях (20.1)-(20.5)) на

 при
при  не меняются. При этом все
значения
не меняются. При этом все
значения  остаются целыми и во все время работы алгоритма
удовлетворяют
неравенствам
остаются целыми и во все время работы алгоритма
удовлетворяют
неравенствам  . Таким образом, мы оценили
множество чисел,
которые могут появляться в вычислениях в качестве знаменателей.
. Таким образом, мы оценили
множество чисел,
которые могут появляться в вычислениях в качестве знаменателей.Для оценки числителей достаточно найти верхнюю грань для величин  ,
,  и
и  . Первая
из этих величин
оценивается просто: в начале работы алгоритма выполняются неравенства
. Первая
из этих величин
оценивается просто: в начале работы алгоритма выполняются неравенства  . В процессе работы величина
. В процессе работы величина  не возрастает, для доказательства чего достаточно
заметить, что
изменение векторов
не возрастает, для доказательства чего достаточно
заметить, что
изменение векторов 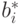 происходит только при перестановке
элементов
базиса, при этом выполняются неравенства
происходит только при перестановке
элементов
базиса, при этом выполняются неравенства  и
и  ,
поскольку
,
поскольку  -
проекция вектора
-
проекция вектора  . Таким образом, во все время работы
алгоритма
. Таким образом, во все время работы
алгоритма  . Оценка величин
. Оценка величин  и
и  существенно
сложнее. Чтобы получить ее, докажем, что всякий раз в точке проверки условия
окончания цикла "пока" выполняются следующие неравенства:
существенно
сложнее. Чтобы получить ее, докажем, что всякий раз в точке проверки условия
окончания цикла "пока" выполняются следующие неравенства:
 |
( 20.17) |
 |
( 20.18) |
 |
( 20.19) |
 |
( 20.20) |
 |
( 20.21) |
При доказательстве этих неравенств пользуемся следующим соотношением:
 |
( 20.22) |
Перед первым выполнением тела цикла неравенства (20.17) и
(20.18) следуют из
неравенства  , которое выполняется по определению
, которое выполняется по определению  . Вместе
с (20.22) это неравенство дает соотношение
. Вместе
с (20.22) это неравенство дает соотношение  , откуда
следует (20.19) и (20.20), а учитывая, что
, откуда
следует (20.19) и (20.20), а учитывая, что  , и
(20.21). Таким образом, перед
первым выполнением тела цикла неравенства (20.17)-(20.21)
справедливы.
, и
(20.21). Таким образом, перед
первым выполнением тела цикла неравенства (20.17)-(20.21)
справедливы.
Предположим теперь, что неравенства (20.17)-(20.21) выполнены
перед началом
выполнения тела цикла, и покажем, что эти неравенства будут выполнены и в
конце тела цикла, т.е. перед выполнением следующего цикла. Неравенство
(20.19)
совпадает с (19.4), которое выполняется для текущего  все время работы
алгоритма A33, в том числе и в начале цикла. Выполнение неравенства
(20.17) для
все время работы
алгоритма A33, в том числе и в начале цикла. Выполнение неравенства
(20.17) для  следует из соотношений (19.1), (20.19) и
неравенства
следует из соотношений (19.1), (20.19) и
неравенства  .
Покажем, что из (20.17) для
.
Покажем, что из (20.17) для  и из неравенства
(20.21) следуют неравенства (20.18)
и (20.20). Доказательство (20.18) сводится к разложению
и из неравенства
(20.21) следуют неравенства (20.18)
и (20.20). Доказательство (20.18) сводится к разложению 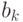 в сумму по формуле
(19.1), применению неравенства (20.21) и вычислению суммы
геометрической
прогрессии. Неравенство (20.20) непосредственно вытекает из (20.22)
и (20.17).
в сумму по формуле
(19.1), применению неравенства (20.21) и вычислению суммы
геометрической
прогрессии. Неравенство (20.20) непосредственно вытекает из (20.22)
и (20.17).
Итак, покажем, что если перед началом выполнения тела цикла
справедливы
неравенства (20.17)-(20.21), то и после его выполнения неравенства
(20.17) и (20.21) также
имеют место. Отдельно рассмотрим два случая: работа алгоритма осуществляется
по ветви "то", т.е. два вектора меняются местами; второй случай -
алгоритм идет на ветвь "иначе", т.е. осуществляется выполнение условия
(19.4)
для всех  .
.
В первом случае множество векторов  не
изменилось (мы
поменяли местами
не
изменилось (мы
поменяли местами  -ый вектор с
-ый вектор с  -ым и уменьшили
после этого
-ым и уменьшили
после этого  на 1).
Во втором случае множество
на 1).
Во втором случае множество  векторов, для которых
нам нужно
доказать неравенство (20.17), заменилось на собственное его
подмножество. Этим
заканчивается индуктивный шаг для неравенства (20.17).
векторов, для которых
нам нужно
доказать неравенство (20.17), заменилось на собственное его
подмножество. Этим
заканчивается индуктивный шаг для неравенства (20.17).
Переходим к оценке  (если
(если  ).
Снова в теле цикла может
выполняться одна из двух серий команд, причем в конце каждой серии значение
переменной
).
Снова в теле цикла может
выполняться одна из двух серий команд, причем в конце каждой серии значение
переменной  меняется, либо увеличиваясь, либо уменьшаясь на 1.
Значение
меняется, либо увеличиваясь, либо уменьшаясь на 1.
Значение  увеличивается, когда алгоритм идет по второй ветви, т.е. достигается
выполнение условия (19.4) для всех
увеличивается, когда алгоритм идет по второй ветви, т.е. достигается
выполнение условия (19.4) для всех  (отдельно, до
цикла достигается это
условие для
(отдельно, до
цикла достигается это
условие для  , в цикле - для
, в цикле - для  ).
Эти операции никак не влияют на
).
Эти операции никак не влияют на  , если
, если  , в частности, при
, в частности, при  . На следующем шаге
значение
. На следующем шаге
значение  увеличивается на 1, и неравенства (20.21) следуют
из (20.20), которые
выполняются на предыдущем этапе.
увеличивается на 1, и неравенства (20.21) следуют
из (20.20), которые
выполняются на предыдущем этапе.
Значение  уменьшается на 1, если в теле цикла выполняется
перестановка
векторов, при этом после ее выполнения новые значения коэффициентов
уменьшается на 1, если в теле цикла выполняется
перестановка
векторов, при этом после ее выполнения новые значения коэффициентов  совпадают со старыми значениями (с учетом замены
совпадают со старыми значениями (с учетом замены  на
на  ). Остается
только проследить, как изменилось значение коэффициентов
). Остается
только проследить, как изменилось значение коэффициентов  , когда
до перестановки векторов мы добивались выполнения условия (19.4)
для
, когда
до перестановки векторов мы добивались выполнения условия (19.4)
для  . При этом к
. При этом к  -ой строке матрицы
-ой строке матрицы  прибавлялась (
прибавлялась (  )-я
строка, умноженная на
)-я
строка, умноженная на  , где
, где  . Учитывая, что
. Учитывая, что  , получаем
, получаем
 |
( 20.23) |
Поскольку новое значение  на 1 меньше старого, получаем
требуемую формулу,
доказательство неравенств (20.17)-(20.21) закончено.
на 1 меньше старого, получаем
требуемую формулу,
доказательство неравенств (20.17)-(20.21) закончено.
Для завершения доказательства предложения 20.4 нам осталось только оценить
значения, получающиеся на промежуточных этапах алгоритма. Заметим, что при
выполнении алгоритма A35 значения
коэффициентов  не более, чем
удваиваются. Поскольку в одном теле основного цикла алгоритм A35 выполняется
не более, чем
не более, чем
удваиваются. Поскольку в одном теле основного цикла алгоритм A35 выполняется
не более, чем  раз, то
раз, то

откуда, воспользовавшись формулами (19.1),
ортогональностью векторов 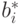 , неравенствами
, неравенствами  получаем
неравенства
получаем
неравенства  для
для  . Остается
перемножить границы для знаменателей и для абсолютных величин,
прологарифмировать и выделить главную часть, чтобы получить оценки,
фигурирующие в предложении 20.4.
. Остается
перемножить границы для знаменателей и для абсолютных величин,
прологарифмировать и выделить главную часть, чтобы получить оценки,
фигурирующие в предложении 20.4.
