|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Лекция 10: Алгоритмы факторизации, основанные на выборе малого вектора в решетке
Рассмотрим на кольце многочленов ![\mathbb R [x]](/sites/default/files/tex_cache/f786072cb0aef1ad765b08b36e02b83c.png) фильтрацию по
степеням
многочленов, т.е. для любого неотрицательного целого
фильтрацию по
степеням
многочленов, т.е. для любого неотрицательного целого  векторное
пространство, состоящее из многочленов степени не выше
векторное
пространство, состоящее из многочленов степени не выше  ,
обозначается
,
обозначается ![\mathbb R _s [x]](/sites/default/files/tex_cache/3af6108b9b5d0aa0b6644a517893ed04.png) . Введенная фильтрация индуцирует фильтрацию на кольце
. Введенная фильтрация индуцирует фильтрацию на кольце ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) :
: ![\mathbb Z _s [x] = \mathbb Z [x] \bigcap \mathbb R _s [x]](/sites/default/files/tex_cache/39614652ef4fdfd85d4146cfd97fd9d7.png) .
. ![\mathbb R _s [x]](/sites/default/files/tex_cache/3af6108b9b5d0aa0b6644a517893ed04.png) образует
вещественное линейное
пространство размерности
образует
вещественное линейное
пространство размерности  , а
, а ![\mathbb Z _s [x]](/sites/default/files/tex_cache/95c8fc9e5c7f6251499b6dca94f86dc7.png) является в нем решеткой
(свободным
является в нем решеткой
(свободным 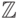 -модулем максимального ранга).
-модулем максимального ранга).
Рассмотрим целое число 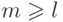 . Через
. Через 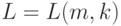 обозначим множество
всех многочленов в кольце
обозначим множество
всех многочленов в кольце ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) , которые делятся на
, которые делятся на 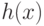 по модулю
по модулю 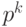 и степень которых не превосходит
и степень которых не превосходит  , т.е.
, т.е. ![L(m,k) = \mathbb Z _m [x]
\bigcap \varphi_k^{-1} ((\varphi_k (h)))](/sites/default/files/tex_cache/a3047c3fbb7448ab95f68b5e105451d5.png) . Другими словами,
. Другими словами,  состоит из
тех многочленов, коэффициенты остатков от деления которых на
состоит из
тех многочленов, коэффициенты остатков от деления которых на 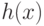 в
в  - адической метрике не превосходят
- адической метрике не превосходят 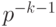 , т.е. являются малыми
величинами. Легко видеть, что базис решетки
, т.е. являются малыми
величинами. Легко видеть, что базис решетки  образует
следующее
множество многочленов
образует
следующее
множество многочленов
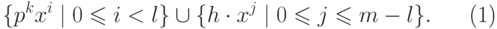 |
( 21.25) |
 удобно выбрать одночлены
удобно выбрать одночлены 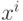 ,
, 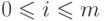 . Длиной
многочлена назовем евклидову длину этого многочлена в выбранном базисе,
который мы предполагаем ортонормированным. Oтождествляем многочлен с
вектором его коэффициентов в выделенном базисе. Матрица коэффициентов
базиса (21.25) имеет в этом базисе треугольную форму и легко видеть,
что
. Длиной
многочлена назовем евклидову длину этого многочлена в выбранном базисе,
который мы предполагаем ортонормированным. Oтождествляем многочлен с
вектором его коэффициентов в выделенном базисе. Матрица коэффициентов
базиса (21.25) имеет в этом базисе треугольную форму и легко видеть,
что 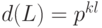 .
Покажем, что элементы решетки
.
Покажем, что элементы решетки  с малой длиной лежат в главном
идеале,
порожденном многочленом
с малой длиной лежат в главном
идеале,
порожденном многочленом  в
в ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) .
.21.4. ПРЕДЛОЖЕНИЕ. Предположим, что многочлен 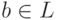 удовлетворяет
неравенству
удовлетворяет
неравенству
 |
( 21.26) |
 делится на
делится на  в кольце
в кольце ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) , в частности,
, в частности, 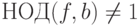 .
.ДОКАЗАТЕЛЬСТВО. Можно считать, что  . Положим
. Положим  .
Достаточно показать, как следует из предыдущего предложения, что
.
Достаточно показать, как следует из предыдущего предложения, что  . Предположим противное.
Пользуясь
неприводимостью
. Предположим противное.
Пользуясь
неприводимостью 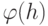 и эпиморфностью гомоморфизма
и эпиморфностью гомоморфизма  ,
получаем существование многочленов
,
получаем существование многочленов ![u,v,w \in \mathbb Z [x]](/sites/default/files/tex_cache/3fbc69b4ba00214644a086a82bb0c715.png) , таких, что
, таких, что
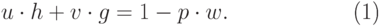 |
( 21.27) |
Напомним, что  ,
,  ,
, 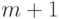 -
размерность решетки
-
размерность решетки  . Положим
. Положим  и
и  .
.
Очевидно, что 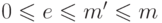 . Положим
. Положим 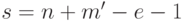 .
.
Пусть ![M_f = \mathbb Z _s [x] \cap (f), M_b = \mathbb Z _s [x] \cap (b)](/sites/default/files/tex_cache/b8d6a1a9f4734da116325c0aef8ea6b3.png) , и
, и 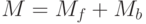 , т.е.
, т.е.  является
является 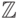 -модулем, состоящим
из всех многочленов вида
-модулем, состоящим
из всех многочленов вида  , где
, где ![u \in \mathbb Z _{m'-e-1} [x]](/sites/default/files/tex_cache/da0aceb74a9ea0ef403722f00ad7eaf5.png) ,
, ![v \in \mathbb Z _{n-e-1}[x]](/sites/default/files/tex_cache/ea1117b0bec59c3b1a4658f6a30678fc.png) .
.
Покажем, что множество элементов
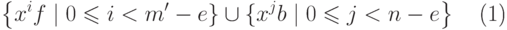 |
( 21.28) |
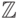 -модуля
-модуля  . Очевидно, что они
порождают
. Очевидно, что они
порождают  , остается
только показать, что выписанная система многочленов линейно независима над
, остается
только показать, что выписанная система многочленов линейно независима над 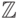 . Предположим, что
. Предположим, что 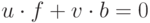 , где
, где 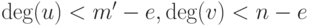 . Разделим это соотношение на
. Разделим это соотношение на  .
Получим,
.
Получим, 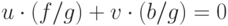 . Пользуясь взаимной простотой многочленов
. Пользуясь взаимной простотой многочленов  и
и 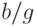 и ограничениями на степени
и ограничениями на степени  и
и  ,
получаем, что
,
получаем, что  .
.Рассмотрим проекцию
![\begin{equation}
\pi\colon \mathbb R _s [x] \to \mathbb R _s [x]/\mathbb R _{e-1}[x].
\end{equation}](/sites/default/files/tex_cache/71c66611ab0deceb001e09dfec5fe99d.png) |
( 21.29) |
Пусть 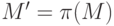 . Покажем, что
. Покажем, что 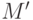 -
решеткa в
-
решеткa в ![\mathbb R _s [x]/\mathbb R _{e-1} [x]](/sites/default/files/tex_cache/15ba5f0718a3ef12ae84e2302e9e58b9.png) . Для
этого достаточно показать, что
. Для
этого достаточно показать, что  , т.е.
, т.е. ![M
\cap
\mathbb Z _{e-1} [x] = 0](/sites/default/files/tex_cache/82135dfdaace11db492174fed44e0633.png) . Пусть
. Пусть ![w \in M \cap \mathbb Z _{e-1} [x]](/sites/default/files/tex_cache/19a66917bef4f05a1e10e0559651dee1.png) ,
тогда
,
тогда 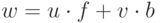 по определению
по определению  , следовательно,
, следовательно,  делится на
делится на 
 . Поскольку
. Поскольку 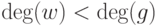 , получаем
, получаем  . Учитывая
линейную независимость элементов множества (21.28) над
. Учитывая
линейную независимость элементов множества (21.28) над 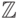 ,
получаем, что
эти элементы образуют базис решетки
,
получаем, что
эти элементы образуют базис решетки 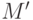 . Неравенство Адамара
(19.3)
утверждает, что
. Неравенство Адамара
(19.3)
утверждает, что 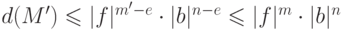 . Пользуясь предположением теоремы, получаем
. Пользуясь предположением теоремы, получаем 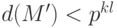 .
.
Для получения желаемого противоречия, покажем, что из (21.27)
следует
обратное неравенство 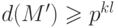 .
.
Покажем, что для любого элемента 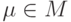 , если
, если 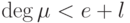 , то
, то 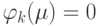 , т.е.
, т.е. 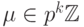 . Домножим
соотношение (21.27) на
. Домножим
соотношение (21.27) на  . Получим
. Получим ![u_1\cdot h+v_1\cdot\mu\equiv
\mu/g\pmod{p^k \mathbb Z [x]}](/sites/default/files/tex_cache/35122eb5353297a4ddae99c8c30e2ebc.png) , где
, где 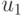 ,
, 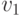 -
некоторые многочлены из кольца
-
некоторые многочлены из кольца ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) . Поскольку\break
. Поскольку\break 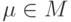 ,
,  делится на
делится на 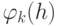 ,
следовательно,
,
следовательно, 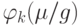 также делится на
также делится на 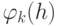 .
Сравнивая степени, получаем, что
.
Сравнивая степени, получаем, что 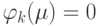 .
.
Для завершения доказательства достаточно теперь показать, что базис 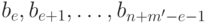 решетки
решетки 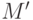 можно выбрать
таким образом, что
можно выбрать
таким образом, что 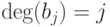 . Это упражнение на приведение невырожденной
целочисленной
матрицы к треугольному виду оставляется читателю. При таком выборе базиса,
старшие коэффициенты первых
. Это упражнение на приведение невырожденной
целочисленной
матрицы к треугольному виду оставляется читателю. При таком выборе базиса,
старшие коэффициенты первых  многочленов делятся на
многочленов делятся на 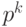 . Значит
. Значит 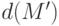 , который в полученном базисе равен произведению
старших
коэффициентов, удовлетворяет неравенству
, который в полученном базисе равен произведению
старших
коэффициентов, удовлетворяет неравенству 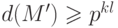 ,
что
завершает доказательство теоремы.
,
что
завершает доказательство теоремы.
Следующий результат позволяет находить неприводимый делитель многочлена  .
.
21.5. ПРЕДЛОЖЕНИЕ.
Пусть  ,
,  ,
,  ,
,  ,
,  ,
,  выбраны так, как предполагалось в
начале параграфа,
выбраны так, как предполагалось в
начале параграфа,  - решетка, заданная базисом
(21.25). Предположим, что
- решетка, заданная базисом
(21.25). Предположим, что 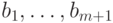 - редуцированный базис решетки
- редуцированный базис решетки  и что выполняется
неравенство
и что выполняется
неравенство
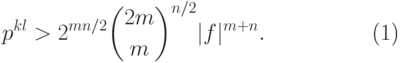 |
( 21.30) |
Если  - неприводимый над
- неприводимый над 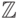 многочлен,
делящийся на
многочлен,
делящийся на  , то
, то 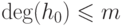 тогда и только тогда, когда
тогда и только тогда, когда
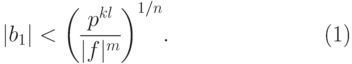 |
( 21.31) |
ДОКАЗАТЕЛЬСТВО.
Если условие (21.31) выполнено, то по предложению 21.4
многочлен 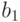 делится на
делится на  . Решетка
. Решетка  выбрана так, что
выбрана так, что 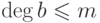 для любого
для любого 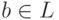 , следовательно,
, следовательно, 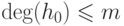 .
.
Предположим теперь, что 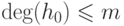 . Тогда
. Тогда 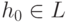 по предложению 21.4.
по предложению 21.4.
Полагая  в предложении 19.9, получим
в предложении 19.9, получим 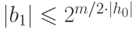 .
.
Теперь из задачи 7.6 следует
неравенство 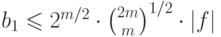 .
Подставляя сюда (21.30), получим (21.31).
.
Подставляя сюда (21.30), получим (21.31).
Теперь можно сформулировать следующий алгоритм нахождения неприводимого
в ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) многочлена, делящегося по модулю
многочлена, делящегося по модулю  на
неприводимый по модулю
на
неприводимый по модулю  многочлен
многочлен 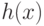 .
.
