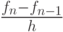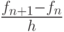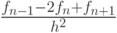НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 7: Интерполяция функций

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский физико-технический институт

|

Вам нравится? Нравится 55 студентам

| Поделиться |

Поддержать программу

Интегрируя последнее соотношение еще раз, получаем:

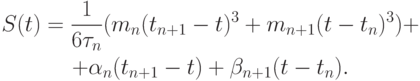
$\begin{gather*} S(t) = \frac {1}{6\tau_n} (m_n (t_{n + 1} - t)^3 + m_{n + 1} (t - t_n)^3) + \\ + \alpha_n (t_{n + 1} - t) + \beta_{n + 1} (t - t_n ). \end{gather*}$

A_n — константа интегрирования. После второго интегрирования положим $A_n t + B_n = (\beta_n - \alpha_n)t + \alpha_n t_{n + 1} - \beta_n t_n ,$ т.е. вместо двух констант A_n, B_n введем две новые константы, более удобные для дальнейших выкладок.

Из условий S(t_n) = f_n, S(t_{n + 1}) = f_{n + 1}, получаем:

$\begin{gather*} f_n = \frac{{m_n \tau_n^2 }}{6} + \alpha {}_n\tau_n \Rightarrow \alpha_n = \frac{{f_n}}{{\tau_n}} - \frac{{m_n\tau_n}}{6}. \\ f_{n + 1} = \frac{{m_{n + 1} \tau_n^2 }}{6} + \beta {}_n\tau_n \Rightarrow \beta_n = \frac{{f_{n + 1}}}{{\tau_n}} - \frac{{m_{n + 1} \tau_n}}{6}. \\ A_n = \frac{{f_{n + 1} - f_n}}{{\tau_n}} - \frac{{(m_{n + 1} - m_n)\tau_n}}{6}. \end{gather*}$

Приравняем первые производные в t_n справа и слева S'_t(t_n + 0) = S'_t(t_n - 0), получим систему уравнений для определения коэффициентов сплайна:

$\frac{m_n \tau_{n - 1}}{2} - \frac{m_{n - 1} \tau_{n - 1}}{2} + \frac{f_n - f_{n - 1}}{\tau_{n - 1}} - \frac{(m_n - m_{n - 1})\tau_{n - 1}}{6} = \\ {= \frac{m_{n + 1} \tau_n}{2} - \frac{m_n \tau_n}{2} + \frac{f_{n + 1} - f_n}{\tau_n} - \frac{(m_{n + 1} - m_n)\tau_n}{6}, }$

( 6.3)

которая дополняется соответствующими граничными условиями. В случае свободного сплайна m₀ = m_N = 0.

Систему для определения коэффициентов, называемых моментами кубического сплайна, можно записать в матричной форме

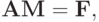
$\mathbf{AM} = \mathbf{F},$

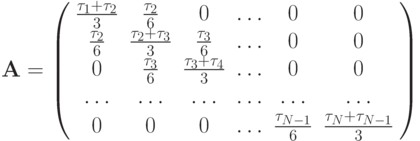
где $\mathbf{A}$ — квадратная матрица:

$\mathbf{A} = \left( \begin{array}{cccccc} {\frac {\tau_1 + \tau_2}{3}} & {\frac {\tau_2}{6}} & 0 & \ldots & 0 & 0 \\ {\frac{\tau_2}{6}} & {\frac {\tau_2 + \tau_3}{3}} & {\frac{\tau_3}{6}} & \ldots & 0 & 0 \\ 0 & {\frac{\tau_3}{6}} & {\frac {\tau_3 + \tau_4}{3}} & \ldots & 0 & 0 \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & 0 & \ldots & {\frac{\tau_{N - 1}}{6}} & {\frac{\tau_N + \tau_{N - 1}}{3}} \\ \end{array} \right)$

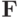$\mathbf{M}$ и $\mathbf{F}$ — векторы - столбцы:

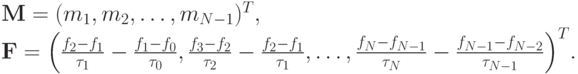
${\mathbf{M}} = (m_1, m_2, \ldots , m_{N - 1})^T , \\ {\mathbf{F}} = {\left(\frac {f_2 - f_1}{\tau_1} - \frac{f_1 - f_0}{\tau_0}, \frac {f_3 - f_2}{\tau_2} - \frac{f_2 - f_1}{\tau_1}, \ldots , \frac {f_N - f_{N - 1}}{\tau_N} - \frac{f_{N - 1} - f_{N - 2}}{\tau_{N - 1}}\right)}^T.$

Матрица $\mathbf{A}$ симметрична, имеет свойство диагонального преобладания и, как можно показать, положительно определена, а следовательно, неособенная. Значит, решение рассматриваемой СЛАУ существует и единственно. Следовательно, и задача о построении кубического сплайна имеет единственное решение. Для других типов краевых условий доказательство проводится аналогично. Метод решения такой СЛАУ, который будет рассмотрен в "Численное решение краевых задач для систем обыкновенных дифференциальных уравнений" — прогонка.

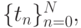Теорема (без доказательства.) Для функции $f(t) \in C^4 [a, b]$ и интерполирующего ее сплайна S (t), построенного на сетке $\{t_n\}_{n = 0}^{N},$ имеют место следующие неравенства:

$\begin{gather*} \left\|{f(t) - S(t)}\right\|_{[a, b]} \le M_4 \tau ^4, \\ \left\|{f^{\prime}(t) - S^{\prime}(t)}\right\|_{[a, b]} \le M_4 \tau ^3, \\ \left\|{f^{\prime\prime}(t) - S^{\prime\prime}(t)}\right\|_{[a, b]} \le M_4 \tau ^2, \end{gather*}$

где M₄ = || f⁽⁴⁾(t) ||_{[a, b]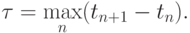}, $\tau = \max\limits_n (t_{n + 1} - t_n).$

Отсюда следует, что при 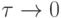$\tau\rightarrow 0$ последовательность функций S^(k)(t), i = 0, 1, 2 (кубический сплайн и первые две его производные) сходится, соответственно, к f^(k)(t).

Теорема (экстремальное свойство кубических сплайнов (без доказательства.) Пусть сплайн S(t) интерполирует функцию f(t) на системе узлов

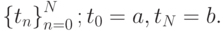
$\left\{{t_n}\right\}_{n = 0}^{N}; t_0 = a, t_N = b.$

Тогда S(t) с краевыми условиями S''(a) = S''(b) = 0 доставляет минимум функционалу

$\int\limits_{a}^{b}{[F^{\prime\prime}(t)]^2 }dt$

среди всех функций $F(t) \in C^2_2 [a, b],$ т.е. функций, имеющих интегрируемые с квадратом вторые производные $(\int\limits_{a}^{b}{{[F^{\prime\prime}(t)]}^2 dt})$ сходится на отрезке [a, b] ) и интерполирующих f(t) на отрезке [a, b].

Локальный сплайн. Локальная форма сплайн - интерполяции предложена В. С. Рябеньким [6.9], [6.10]. Рассмотрим неравномерную сетку: t_n - t_{n - 1} = h_{n - 1}, t_{n + 1} - t_n = h_n. В узлах сетки определены значения функции: f_{n - 1}, f_n , f_{n + 1}. Не вдаваясь в детали, приведем важные для практического использования формулы в случае постоянного шага сетки h = const . Построим интерполяционный полином второго порядка P₂(x) в форме Ньютона (d - f_n)/h:

t_n-1

f_n-1

$\frac{f_n - f_{n - 1}}{h}$

$\frac{f_{n + 1} - f_n}{h}$

$\frac{f_{n - 1} - 2f_n + f_{n + 1}}{h^2}$

t_n

f_n

t_n+1

f_n+1

$\begin{gather*} P_2 (t, f_n) = f_{n - 1} + \frac{{f_n - f_{n - 1}}}{h} (t - t_{n - 1}) + \\ + \frac{f_{n - 1} - 2f_n + f_{n + 1}}{h^2 } (t - t_{n - 1})(t - t_n), \end{gather*}$

( 6.4)

Этот полином приближает f на отрезке [ t_{n - 1}, t_{n + 1} ] с точностью до o(h²). Рассмотрим теперь полином

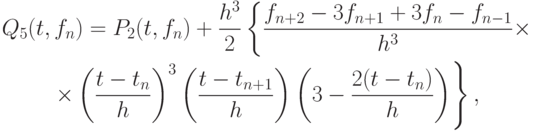
$\begin{gather*} Q_5 (t, f_n) = P_2 (t, f_n) + \frac{h^3}{2} \left\{{\frac{f_{n + 2} - 3f_{n + 1} + 3f_n - f_{n - 1}}{h^3} \times }\right. \\ \left. {\times \left({\frac{t - t_n}{h}}\right)^3 \left({\frac{t - t_{n + 1}}{h}}\right)\left({3 - \frac{2(t - t_n)}{h}}\right)}\right\}, \end{gather*}$

представляющий собой аппроксимацию функции f на отрезке [t_{n - 1}, t_{n + 1}] с непрерывными первой и второй производными. В [6.1] доказано, что выражение (6.4) аппроксимирует 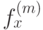$f_x^{(m)}$ с порядком o(h^{3 - m}) во всех точках отрезка. Так как коэффициенты сплайна зависят от значений функции лишь в 4-х соседних точках и для определения коэффициентов (6.4) не требуется решать систему линейных уравнений, такая кусочно - гладкая интерполяция называется локальным сплайном.

Замечание. Q₅(t, f_n) уже не обладает экстремальным свойством.

Дальше >>

Введение в вычислительную математику

Введение в вычислительную математику

Интерполяция функций

Вопросы и ответы

Студенты

Авторизоваться

Введение в вычислительную математику

Введение в вычислительную математику

Интерполяция функций

Вопросы и ответы

Студенты