НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 7: Интерполяция функций

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский физико-технический институт

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать программу

6.14. Задачи для самостоятельного решения

Покажите, что интерполяционный полином в форме Лагранжа может быть построен в соответствии со следующими рекуррентными формулами: L₀(t) = f(t₀),
$\begin{gather*} L_n (t) = L_{n - 1} (t) + \left[{f(t_n) - L_{n - 1} (t)}\right] + \frac{{P_n (t)}}{{P_n (t_n)}}, \\ P_1 (t) = t - t_0, P_{n + 1}(t) = P_n(t)(t - t_n). \end{gather*}$
Построить интерполяционный кубический полином 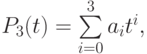$P_3 (t) = \sum\limits_{i = 0}^3{a_i t^{i}} ,$ для которого выполнено P₃(1) = 1, P₃(2) = 2, P₃(3) = 2, a₃ = 1.
Построить интерполяционный полином в форме Лагранжа для функций f(t) = | t |, f(t) = t² по узлам - 1; 0; 1 ; и - 2; - 1; 0; 1; 2.
Оценить погрешность интерполяции функции f(t) = sin t на отрезке $[0;\pi /4]$ по трем равноотстоящим узлам.
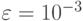Оценить, какое количество узлов интерполяции потребуется на отрезке $[0; \pi /4]$ для обеспечения точности $\varepsilon = 10^{ - 3}$ при интерполяции функции sin t.
Привести примеры непрерывных функций, для которых расходится последовательность интерполяционных полиномов (на равномерной сетке).
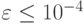Какой величины необходимо выбрать шаг интерполирования $\tau$ для обеспечения точности $\varepsilon \le 10^{- 4}$ интерполяции функции $f(t) = \sqrt[3]{t}, t \in [1;10^3 ]$ при линейной и квадратичной интерполяции?
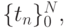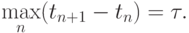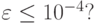Пусть имеется таблица функции f(t) = sin t в равноотстоящих точка $\{t_n\}_0^N,$ причем $\max\limits_n (t_{n + 1} - t_n) = \tau .$ При каком $\tau$ линейная интерполяция позволит восстановить f(t) с точностью $\varepsilon \le 10^{- 4}?$ Тот же вопрос для квадратичной интерполяции. Решить задачу для случаев равномерной и неравномерной сеток $\{t_n\}_0^{N}.$
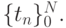
Как оценить погрешность интерполяционного процесса, если интерполируемая функция задана таблично?
По заданным значениям функции

t 1 2 2,5 3

f - 6 - 1 15,6 16

найти значение t, при котором f(t) = 0 (решение уравнения f(t) = 0 для заданной функции методом обратной интерполяции ).
Построить линейный и кубический сплайны по значениям функции f(t) в точках {0, 1} и {0, 1, 2} соответственно.
Показать, что система линейных алгебраических уравнений для определения коэффициентов сплайна (6.3) всегда имеет единственное решение. Показать, что для этой системы устойчив метод прогонки. Оценить число обусловленности системы (6.3) в случае, когда $h_n \equiv h$ не зависит от номера узла.