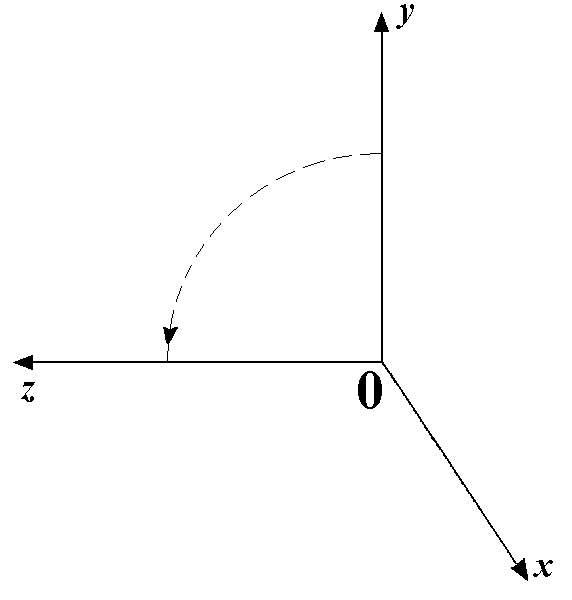Геометрические преобразования

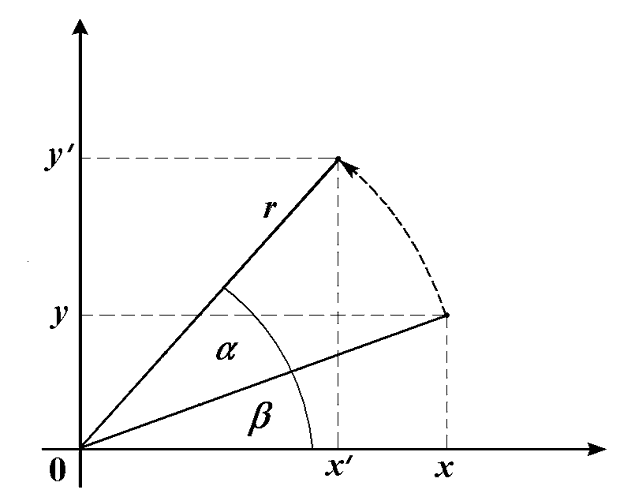
Вращения в плоскости перемещают точки по дуге окружности, центр которой находится в начале координат. Рассмотрим сначала движение одной точки при повороте на угол (положительным является направление против часовой стрелки), т. е. поворот радиус-вектора на угол (рис. 3.7). Пусть точка располагалась на расстоянии от начала координат, а ее радиус-вектор составлял угол с осью абсцисс. Тогда координаты точки определяются формулами

После поворота вектор будет составлять угол , а новые координаты точки будут определяться соотношениями

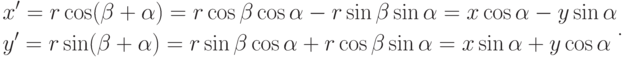( 3.16)

Можно показать, что при таком преобразовании сохраняются расстояния между точками, а следовательно, и углы между отрезками.

Рис. 3.7. Поворот на плоскости

Рис. 3.8. Поворот в пространстве

В случае трехмерного пространства рассуждения, касающиеся переноса и масштабирования, полностью аналогичны, только они распространяются на третью координату точек. С вращением же дело обстоит иначе, поскольку здесь вращательное движение есть перемещение вдоль поверхности сферы и поворот на какой-то угол относительно точки нельзя определить однозначно. Но перемещение из одной точки сферы в другую всегда можно осуществить последовательностью поворотов относительно осей координат, поэтому выведем формулы для этих трех вращений.

При повороте относительно оси 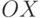на угол у всех точек координата остается неизменной. Если смотреть на плоскость со стороны конца оси 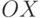, то оси будут расположены так, как показано на рис. 3.8. Положительным считается поворот от 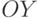оси к оси 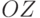. Если воспользоваться формулами для плоских поворотов, то координаты 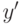и новой точки определяются выражениями

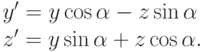
Формулы поворота относит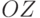ельно оси полностью совпадают с теми, которые были выведены для плоского случая, а поворот относительно оси 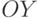выглядит так:

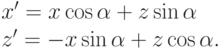
Во всех этих формулах следует обратить внимание на знаки, так как они зависят от того, какой поворот считается положительным (в данном случае мы имеем дело с правой тройкой базисных векторов).

Преобразования масштабирования и поворота на плоскости и в пространстве можно выразить с помощью матриц. Если заданы коэффициенты масштабирования 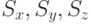, то преобразование точки осуществляется посредством умножения матрицы на ее радиус-вектор,

( 3.8)

Поворот на плоскости можно осуществить с помощью матрицы

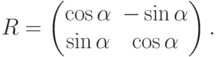( 3.17)

И наконец, повороты в пространстве относительно осей координат можно выполнить с помощью трех матриц вращения

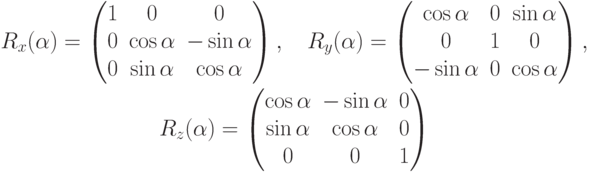( 3.10)

Нетрудно проверить, что для матриц вращения справедливо соотношение

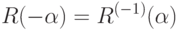
Для выполнения последовательных поворотов вокруг осей на углы 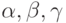можно создать матрицу преобразования путем перемножения трех матриц:

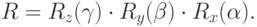
Использование этой матрицы даст заметную экономию в вычислениях по сравнению с последовательными умножениями на каждую из трех матриц вращения.