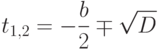Геометрические преобразования
Уравнения прямой и плоскости
Уравнение прямой на плоскости в декартовой системе координат можно задать уравнением вида
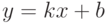
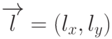 и какую-нибудь точку
и какую-нибудь точку 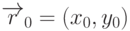 , лежащую на этой прямой. При этом точки, лежащие на
прямой, могут быть заданы с использованием векторных операций в виде
так называемого параметрического уравнения прямой
, лежащую на этой прямой. При этом точки, лежащие на
прямой, могут быть заданы с использованием векторных операций в виде
так называемого параметрического уравнения прямой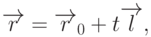
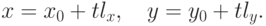 |
( 3.4) |
Прямую в пространстве тоже можно задавать параметрическим
уравнением, которое очень легко получить из предыдущего простым
переходом от двумерных векторов к трехмерным. Пусть 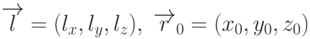 . Тогда это
уравнение будет определять прямую в пространстве, а координаты точек
этой прямой будут определяться формулами
. Тогда это
уравнение будет определять прямую в пространстве, а координаты точек
этой прямой будут определяться формулами
 |
( 3.5) |
Как известно из элементарной геометрии, через любые три точки в пространстве проходит плоскость. С другой стороны, через каждую точку плоскости можно провести единственную прямую, перпендикулярную данной плоскости. При этом все эти прямые будут параллельны друг другу, а значит, они имеют общий вектор направления. Этот вектор будем называть нормалью к плоскости. Если длина вектора равна единице, мы будем называть его единичной нормалью. В компьютерной графике часто приходится решать задачу построения нормали к некоторой плоскости, заданной тремя точками, а также задачи пересечения прямой с плоскостью и двух плоскостей.
Плоскость в пространстве можно задать, указав вектор нормали к ней
и какую-либо точку, принадлежащую данной плоскости. Пусть 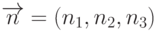 - вектор
единичной нормали, а
- вектор
единичной нормали, а 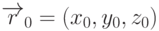 - некоторая точка на плоскости. Тогда для любой
точки
- некоторая точка на плоскости. Тогда для любой
точки 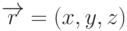 , лежащей на плоскости, вектор
, лежащей на плоскости, вектор 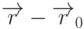 будет ортогонален вектору
нормали, а следовательно, выполняется равенство
будет ортогонален вектору
нормали, а следовательно, выполняется равенство
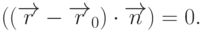
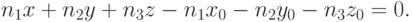
 |
( 3.6) |
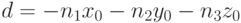 . Это уравнение называется каноническим уравнением плоскости. При
этом совершенно ясно, что если все это уравнение умножить на какой-либо
отличный от нуля множитель, то оно будет описывать ту же самую
плоскость, т.е. коэффициенты
. Это уравнение называется каноническим уравнением плоскости. При
этом совершенно ясно, что если все это уравнение умножить на какой-либо
отличный от нуля множитель, то оно будет описывать ту же самую
плоскость, т.е. коэффициенты 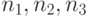 для каждой плоскости задаются с
точностью до произвольного ненулевого множителя. Но если при этом
вектор
для каждой плоскости задаются с
точностью до произвольного ненулевого множителя. Но если при этом
вектор  имеет единичную длину, то
имеет единичную длину, то 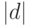 задает расстояние от начала
координат до данной плоскости.
задает расстояние от начала
координат до данной плоскости.В алгоритмах компьютерной графики довольно часто приходится
сталкиваться с задачей построения плоскости, проходящей через три
заданные точки. Пусть три точки 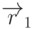 ,
, 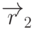 и
и  , не лежащие на одной прямой,
имеют координатами
, не лежащие на одной прямой,
имеют координатами 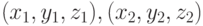 и
и  . Для канонического уравнения необходимо
построить нормаль к плоскости, что легко можно осуществить, используя
операцию векторного произведения. Поскольку векторы
. Для канонического уравнения необходимо
построить нормаль к плоскости, что легко можно осуществить, используя
операцию векторного произведения. Поскольку векторы  и
и 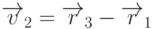 лежат в
искомой плоскости, то вектор
лежат в
искомой плоскости, то вектор 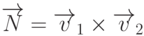 будет ортогонален этой плоскости. Пусть
будет ортогонален этой плоскости. Пусть 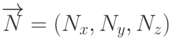 , тогда уравнение плоскости будет иметь вид
, тогда уравнение плоскости будет иметь вид

Остается определить значение  . Так как точка
. Так как точка 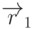 принадлежит этой
плоскости, то ее координаты должны удовлетворять полученному
уравнению. Подставим их в уравнение и получим
принадлежит этой
плоскости, то ее координаты должны удовлетворять полученному
уравнению. Подставим их в уравнение и получим
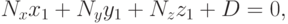

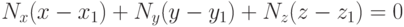 |
( 3.7) |
В большинстве алгоритмов, использующих плоскости, достаточно знать нормаль к ней и какую-либо точку, принадлежащую плоскости. Очевидно, что по аналогии можно вывести каноническое уравнение прямой на плоскости, если задана нормаль к ней и принадлежащая прямой точка.
Пересечение луча с плоскостью и сферой
Прямая на плоскости и в пространстве является бесконечной в обе
стороны. Лучом называется полупрямая, т.е. множество всех точек
прямой, лежащих по одну сторону от заданной ее точки, называемой
началом луча. Луч будем задавать в параметрическом виде, как это было
описано в одном из предыдущих разделов. Пусть 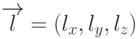 - направляющий вектор
прямой, а
- направляющий вектор
прямой, а 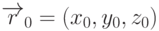 - начальная точка. Тогда координаты точек луча будут
определяться формулами
- начальная точка. Тогда координаты точек луча будут
определяться формулами
 |
( 3.8) |
Будем считать, что направляющий вектор единичный, т.е.  .
.
Сначала рассмотрим задачу о нахождении точки пересечения луча с плоскостью, заданной каноническими уравнением
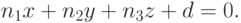 |
( 3.9) |
Вектор нормали 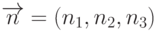 тоже будем считать единичным. Сначала надо
определить значение параметра t, при котором луч пересекает плоскость.
Для этого подставим координаты из формулы (3.8) в уравнение (3.9) и
получим
тоже будем считать единичным. Сначала надо
определить значение параметра t, при котором луч пересекает плоскость.
Для этого подставим координаты из формулы (3.8) в уравнение (3.9) и
получим
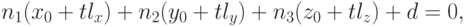
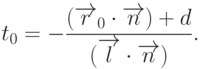
Очевидно, что такая точка существует только при условии 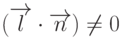 . В свою
очередь, эта величина обращается в нуль только в случае, когда векторы
. В свою
очередь, эта величина обращается в нуль только в случае, когда векторы 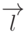 и
и  ортогональны друг другу.
ортогональны друг другу.
Пусть теперь нам задана сфера с центром в точке 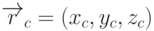 и радиусом
и радиусом 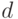 .
Тогда уравнение сферы будет иметь вид
.
Тогда уравнение сферы будет иметь вид

Подставив сюда координаты луча из уравнения (3.8), получим, что параметр, при котором луч пересекает сферу, должен удовлетворять квадратному уравнению
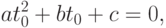
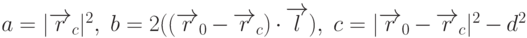 .
Определим корни этого уравнения. Если дискриминант
.
Определим корни этого уравнения. Если дискриминант  , то
корни существуют. Их может быть либо два
, то
корни существуют. Их может быть либо два 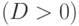 , либо один
, либо один 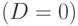 . В
первом случае имеем две точки пересечения, во втором - одну (луч
касается сферы). Соответствующие значения параметра определяются
соотношением
. В
первом случае имеем две точки пересечения, во втором - одну (луч
касается сферы). Соответствующие значения параметра определяются
соотношением