Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений

Устойчивость методов численного интегрирования жестких систем ОДУ обычно исследуется на примере скалярного уравнения

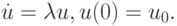( 9.4)

Положим, что численный метод, применяемый к решению этого уравнения, может быть записан в виде

где R(z) называется функцией устойчивости [9.1], [9.4]. О построении функции устойчивости речь пойдет ниже.

Определение. Численный метод для решения уравнения (9.4) является абсолютно устойчивым, если выполнено условие

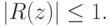
Из определения следует, что

Это требование является естественным при поскольку в таком случае модуль точного решения есть невозрастающая функция.

Множество всех точек z, для которых называется областью абсолютной устойчивости.

Рис. 9.1.

Рис. 9.2a.

Рис. 9.2b.

Рис. 9.3.

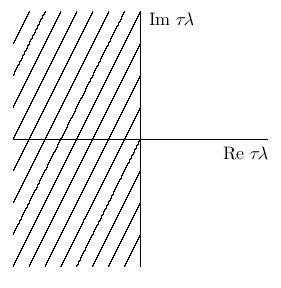
Определение. Если область абсолютной устойчивости занимает левую полуплоскость комплексной плоскости то метод является А - устойчивым (заштрихованная область на рис. 9.1).

В случае, когда область абсолютной устойчивости включает в себя угол (в левой полуплоскости комплексной плоскости) с вершиной в нуле и углом полураствора 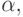то метод называется 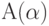- устойчивым.

Области - и A(0) - устойчивости изображены на рис. 9.2а и 9.2b, соответственно.

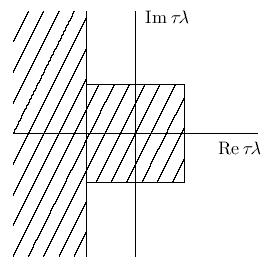
В случае, когда вся область абсолютной устойчивости включает в себя часть левой полуплоскости (граница ее лежит вне заштрихованной части на рис. 9.3), то метод называется жестко - устойчивым. Область жесткой устойчивости имеет вид, представленный, например, на рис. 9.3.

Определение. Численный метод называется L - устойчивым, если он А - устойчив и если

В частности, рассмотренный выше неявный метод Эйлера является L - устойчивым. Решения, полученные такими методами, будут затухающими.