НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: свободно

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать

| Скачать электронную книгу

9.3. Решение линейных ЖС ОДУ и вычисление матричной экспоненты

Рассмотрим один из наиболее простых численных методов решения жестких линейных систем ОДУ [9.10], основанный на представлении решения в явном виде

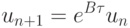
$u_{n + 1} = e^{B\tau }u_{n}$

для линейных систем жестких ОДУ вида

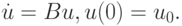
$\dot {u} = Bu, {u}(0) = u_0 .$

Его численная реализация связана с вычислением матричной экспоненты. О свойствах матричной экспоненты (и в целом функций от матриц) можно прочитать в [9.11]. Использование для этого разложения в ряд Тейлора

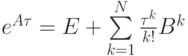
$e^{A{\tau}} = {E} + \sum\limits_{k = 1}^{N}{\frac{\tau^k}{k!}{B}^{k}}$

представляется непригодным, так как простые оценки показывают, что по вычислительным затратам этот алгоритм сопоставим с методом Эйлера с шагом $\tau || B || < 1$ :

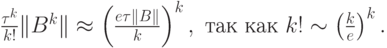
$\frac{{{\tau}^{k}}}{{k!}}\|{B}^{k}\| \approx \left({\frac{e\tau\|{B}\|}{k}}\right)^{k}, \mbox{ так как } k! \sim \left({\frac{k}{e}}\right)^{k} .$

Следовательно, для того, чтобы k - й член разложения ряда Тейлора был, по крайней мере, порядка O(1), необходимо выполнение условия

$\frac{{e\tau\|{B}\|}}{k} \sim O(1), \mbox{ или } \tau\|{B}\| \sim O(1),$

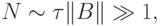что соответствует условию численного интегрирования с шагом $\tau || B || < 1\}.$ Количество членов ряда при этом $N \sim \tau\|{B}\| \gg 1,$ что неприемлемо для решения.

Представим экспоненту в следующем эквивалентном виде:

$e^{{B}{\tau}} = (e^{{\tau}A/2^p})^{2^p} \approx {\left[{E + \frac{{\tau}}{2^p}B + \ldots + \frac{1}{k!}{\left({\frac{{\tau}}{2^p}}\right)}^k B^k}\right]}^{2^p}.$

При этом значение параметра p выбирают таким, чтобы

$\frac{{\tau\|{B}\|}}{{2^{p}}} \ll 1$

и можно было использовать ряд Тейлора с небольшим количеством членов. Действительно, в этом случае

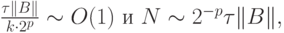
$\frac{{\tau\|{B}\|}}{{k \cdot 2^{p}}} \sim O(1) \mbox{ и } N \sim 2^{- p} \tau\|{B}\|,$

что вполне приемлемо при соответствующем выборе параметра p.

В этом алгоритме сначала вычисляют матрицу

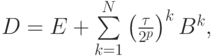
$D = E + \sum\limits_{k = 1}^N{\left({\frac{\tau}{2^p}}\right)^k B^k},$

затем $D^{2^p}$ путем последовательных перемножений. При таком способе вычисления матрицы также имеется опасность, связанная с тем, что при некоторых p, $\lambda _{0}, \Lambda _{0}$ слагаемые, соответствующие мягкой части спектра, окажутся много меньше единицы (и слагаемых, соответствующих жесткой части). В этом случае предпочтение отдается представлению

$e^{A{\tau}} = \left[{\exp \left({- \frac{{\tau}}{2^p}{B}}\right)^{- 1}}\right]^{2^{p}},$

а последовательность вычислений имеет вид

$D = E + \frac{{\tau}}{2^p}B; C = D^{- 1}; C^{\prime} = {(C^2 )}^p .$

При этом на мягкой части спектра, поскольку 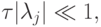${\tau}|\lambda_j | \ll 1,$ имеем

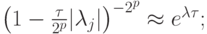
$\left({1 - \frac{{\tau}}{{2^{p}}} |\lambda_j|}\right)^{- 2^{p}} \approx e^{\lambda {\tau}} ;$

на жесткой части, поскольку теперь p небольшие и 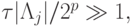${\tau}|{\Lambda_j}|/2^p \gg 1,$ получим оценку

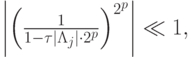
$\left|{\left({\frac{1}{1 - {\tau}|\Lambda_j | \cdot 2^p}}\right)^{2^p}}\right| \ll 1,$

что уже приемлемо для вычислений.

Дальше >>

Введение в вычислительную математику

Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений

9.3. Решение линейных ЖС ОДУ и вычисление матричной экспоненты

Вопросы и ответы

Студенты

Авторизоваться

Введение в вычислительную математику

Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений

9.3. Решение линейных ЖС ОДУ и вычисление матричной экспоненты

Вопросы и ответы

Студенты