| Какие объекты исследует вычислительная математика |
Численное решение систем линейных алгебраических уравнений
К численному решению систем линейных алгебраических уравнений (СЛАУ) сводятся многие задачи математической физики. Математические модели, представляющие собой СЛАУ большой размерности, встречаются в математической экономике, биологии и т.п. Теория получения приближенных решений СЛАУ — часть вычислительной линейной алгебры. Сама вычислительная линейная алгебра, по-видимому, является наиболее обширной темой во всем курсе вычислительной математики. По прикладной линейной алгебре существует обширная литература (например, [2.1, 2.2, 2.3, 2.4, 2.5], а программы, реализующие наиболее популярные алгоритмы вычислительной линейной алгебры, являются неотъемлемой частью прикладного программного обеспечения, в частности, современных математических пакетов.
2.1. Постановка задачи
Рассмотрим СЛАУ вида
 |
( 2.1) |
где  — невырожденная (
— невырожденная (  ) квадратная матрица размером n x n
) квадратная матрица размером n x n
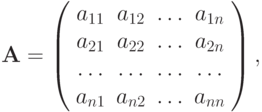
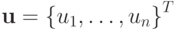 — вектор-столбец решения,
— вектор-столбец решения,  — вектор-столбец правой части.
— вектор-столбец правой части.
Так как матрица системы — невырожденная,  , то решение системы (2.1) существует и единственно.
, то решение системы (2.1) существует и единственно.
Из курса линейной алгебры [2.6] известно правило Крамера нахождения решения. Так, каждый компонент вектора неизвестных может быть вычислен как
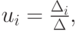
где  — определитель матрицы, получаемой из
— определитель матрицы, получаемой из  заменой i столбца столбцом правых частей. Однако несложные арифметические оценки позволяют понять, что использование этой формулы приводит к неоправданно большим затратам машинного времени [2.3]. Так, например, если одно слагаемое в
заменой i столбца столбцом правых частей. Однако несложные арифметические оценки позволяют понять, что использование этой формулы приводит к неоправданно большим затратам машинного времени [2.3]. Так, например, если одно слагаемое в  вычисляется за 10 -6 с, то время расчета для n = 100 на существующих в момент написания книги компьютерах будет измеряться годами.
вычисляется за 10 -6 с, то время расчета для n = 100 на существующих в момент написания книги компьютерах будет измеряться годами.
На самом деле в настоящее время с помощью компьютеров численно решаются СЛАУ намного более высокого порядка (примерно до 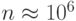 ). Такие решения осуществляются при помощи прямых или итерационных численных методов. Прямые методы позволяют в предположении отсутствия ошибок округления (при проведении расчетов на идеальном, т.е. бесконечноразрядном компьютере) получить точное решение задачи за конечное число арифметических действий Итерационные методы, или методы последовательных приближений, позволяют вычислить последовательность
). Такие решения осуществляются при помощи прямых или итерационных численных методов. Прямые методы позволяют в предположении отсутствия ошибок округления (при проведении расчетов на идеальном, т.е. бесконечноразрядном компьютере) получить точное решение задачи за конечное число арифметических действий Итерационные методы, или методы последовательных приближений, позволяют вычислить последовательность  , сходящуюся к решению задач при
, сходящуюся к решению задач при  (на практике, разумеется, ограничиваются конечным k, в зависимости от требуемой точности).
(на практике, разумеется, ограничиваются конечным k, в зависимости от требуемой точности).
Однако неточность в задании правых частей и элементов матрицы  может приводить к значительным погрешностям при вычислении решения (2.1). В
"Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования"
на примере было показано, что такое явление наблюдается в случае плохо обусловленной системы. Остановимся подробнее на важном вопросе оценки погрешности решения СЛАУ.
может приводить к значительным погрешностям при вычислении решения (2.1). В
"Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования"
на примере было показано, что такое явление наблюдается в случае плохо обусловленной системы. Остановимся подробнее на важном вопросе оценки погрешности решения СЛАУ.
Для этого напомним некоторые сведения из функционального анализа, которые понадобятся в дальнейшем.
2.2. Согласованные нормы векторов и матриц
В векторном n -мерном линейном нормированном пространстве введем следующие нормы вектора:
кубическая:
 |
( 2.2а) |
октаэдрическая:
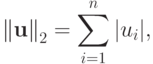 |
( 2.2б) |
евклидова (в комплексном случае — эрмитова):
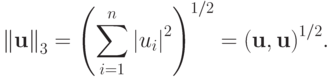 |
( 2.2в) |
Рассмотрим квадратную матрицу  и связанное с ней линейное преобразование
и связанное с ней линейное преобразование 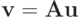 , где
, где  ( Ln — n -мерное линейное нормированное пространство). Норма матрицы определяется как действительное неотрицательное число, характеризующее это преобразование и определяющееся как
( Ln — n -мерное линейное нормированное пространство). Норма матрицы определяется как действительное неотрицательное число, характеризующее это преобразование и определяющееся как
 |
( 2.3) |
Укажем некоторые свойства нормы матрицы:
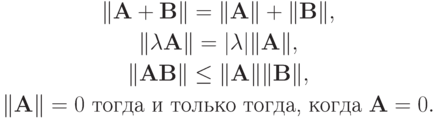
Заметим, что норму матрицы (2.3) называют подчиненной норме вектора. Говорят, что норма матрицы  согласована с нормой вектора
согласована с нормой вектора  , если выполнено условие
, если выполнено условие

Нетрудно видеть, что подчиненная норма согласована с соответствующей метрикой векторного пространства. В самом деле
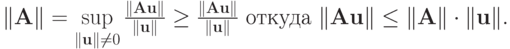
Согласованные с введенными выше нормами векторов нормы матриц будут определяться следующим образом:
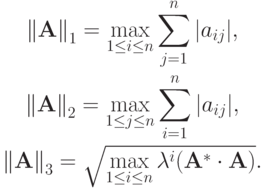
Покажем, как получается выражение для согласованной нормы матрицы  , соответствующей норме вектора
, соответствующей норме вектора 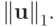
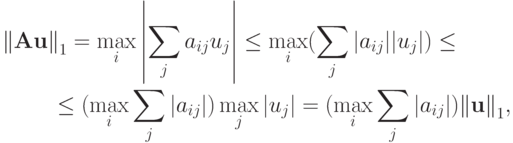
откуда
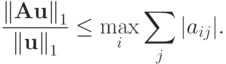
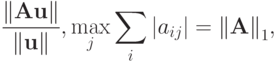
Покажем, что таким вектором является, например,
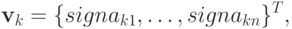
Поскольку 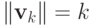 , то
, то 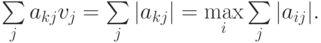
Тогда, в соответствии с выражением для первой нормы вектора, получаем
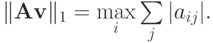
Таким образом, точная верхняя грань в рассмотренном неравенстве достижима и
действительно 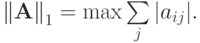
Для третьей нормы (2.2в)
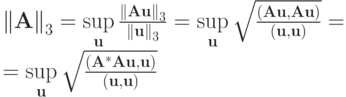
Заметим, что матрица 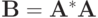 — симметричная. Без ограничения общности предположим, что все собственные числа матрицы различны. Матрица обладает всеми действительными собственными значениями,
и каждому собственному числу соответствует собственный вектор. Все собственные векторы взаимно ортогональны. Можно рассмотреть ортонормированную систему собственных векторов
— симметричная. Без ограничения общности предположим, что все собственные числа матрицы различны. Матрица обладает всеми действительными собственными значениями,
и каждому собственному числу соответствует собственный вектор. Все собственные векторы взаимно ортогональны. Можно рассмотреть ортонормированную систему собственных векторов  — соответствующие им собственные значения. Любой вектор
— соответствующие им собственные значения. Любой вектор  можно представить в виде своего разложения по базису из собственных векторов:
можно представить в виде своего разложения по базису из собственных векторов:  Кроме того,
Кроме того, 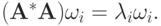 Поэтому
Поэтому
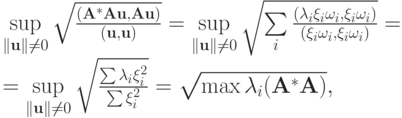
причем точная верхняя грань достигается при 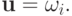 Действительно,
Действительно,

т.к.  , откуда
, откуда 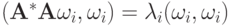 ,
,
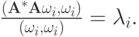
В важном частном случае симметричной (самосопряженной) матрицы  имеем
имеем 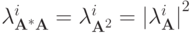 , поэтому
, поэтому 

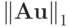 :
: