| Что такое сеть? |
Паросочетания и свадьбы
Приложение теоремы Холла
Рассмотрим приложения теоремы Холла в различных областях.
Латинские квадраты
Латинским 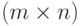 - прямоугольником называется
(
- прямоугольником называется
(  )-матрица
)-матрица 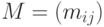 , элементами которой
являются целые числа, удовлетворяющие условиям (1)
, элементами которой
являются целые числа, удовлетворяющие условиям (1)  , (2) все
элементы в каждой строке и в каждом столбце различны . Заметим, что из
условий (1) и (2) следует, что
, (2) все
элементы в каждой строке и в каждом столбце различны . Заметим, что из
условий (1) и (2) следует, что  ; если
; если  , то
латинский прямоугольник называется латинским квадратом. К примеру, ниже изображены латинский
, то
латинский прямоугольник называется латинским квадратом. К примеру, ниже изображены латинский  -прямоугольник и
латинский
-прямоугольник и
латинский  -квадрат. Можно задать следующий вопрос:
если дан латинский
-квадрат. Можно задать следующий вопрос:
если дан латинский 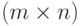 -прямоугольник, где
-прямоугольник, где  ,
когда можно присоединить к нему
,
когда можно присоединить к нему  новых строк так, чтобы получился
латинский квадрат? Удивительно, что ответ на этот вопрос "всегда"!
новых строк так, чтобы получился
латинский квадрат? Удивительно, что ответ на этот вопрос "всегда"!
![\left[\begin{matrix}
1 & 2 & 3 & 4 & 5\\
2 & 4 & 1 & 5 & 3\\
3 & 5 & 2 & 1 & 4
\end{matrix}\right]](/sites/default/files/tex_cache/a112b250823430211aec2bfcbe287b7b.png)
![\left[\begin{matrix}
1 & 2 & 3 & 4 & 5\\
2 & 4 & 1 & 5 & 3\\
3 & 5 & 2 & 1 & 4\\
4 & 3 & 5 & 2 & 1\\
5 & 1 & 4 & 3 & 2
\end{matrix}\right]](/sites/default/files/tex_cache/78c98340c94dd0813837d3bee50e9c6b.png)
Латинские квадраты долгое время были известны лишь математикам и любителям головоломок и, в основном, благодаря одной знаменитой задаче Л. Эйлера1Леонард Эйлер (1707-1783) — один из великих математиков XVIII века, создавших основы математического анализа. Швейцарец по происхождению, он жил и работал преимущественно в России. Эйлер, выделявшийся своей исключительной интуицией и разносторонностью интересов, оставил глубокий след практически во всех областях современной ему математики. Большое количество его замечательных результатов послужило основой для дальнейшего развития многих разделов математики. В 1782 г. Эйлер предложил следующую проблему.
Среди 36 офицеров находится по шесть офицеров шести различных званий из шести полков. Можно ли построить этих офицеров в каре так, чтобы в каждой колонне и каждой шеренге встречались офицеры всех званий и всех полков?
Лишь в 1901 г. удалось доказать, что это невозможно. Однако связанные с задачей Эйлера латинские квадраты не потеряли интереса, так как вскоре обнаружилось, что они имеют многообразные практические применения. А в конце 60-х годов двадцатого столетия они были применены в теории кодирования. Получающиеся на их основе коды допускают простые алгоритмы декодирования.

