| Что такое сеть? |
Бесконечные графы
Краткий обзор свойств бесконечных эйлеровых графов
Связный бесконечный граф  называется эйлеровым,
если в нем существует бесконечная в обе стороны цепь, содержащая каждое ребро
графа
называется эйлеровым,
если в нем существует бесконечная в обе стороны цепь, содержащая каждое ребро
графа  . Такая бесконечная цепь называется (двусторонней) эйлеровой цепью. Назовем граф
. Такая бесконечная цепь называется (двусторонней) эйлеровой цепью. Назовем граф  полуэйлеровым,
если в нем существует бесконечная (в одну или в обе стороны) цепь, содержащая каждое
ребро графа
полуэйлеровым,
если в нем существует бесконечная (в одну или в обе стороны) цепь, содержащая каждое
ребро графа  .
.
Теорема 6.3.
Пусть  — связный счетный граф, являющийся эйлеровым. Тогда:
— связный счетный граф, являющийся эйлеровым. Тогда:
- В графе
 нет вершин нечетной степени.
нет вершин нечетной степени. - Для каждого конечного подграфа
 графа
графа  бесконечный граф
бесконечный граф  (полученный путем удаления из
(полученный путем удаления из  ребер графа
ребер графа  )
имеет не более двух бесконечных связных компонент.
)
имеет не более двух бесконечных связных компонент. - Если, кроме того, степень любой вершины из
 четна,
то
четна,
то  имеет ровно одну бесконечную связную компоненту.
имеет ровно одну бесконечную связную компоненту.
Доказательство
- Предположим, что
 — эйлерова цепь в графе
— эйлерова цепь в графе  . Тогда при всяком прохождении цепи
. Тогда при всяком прохождении цепи  через любую из вершин графа степень этой
вершины увеличивается на два. А так как каждое ребро встречается в
через любую из вершин графа степень этой
вершины увеличивается на два. А так как каждое ребро встречается в  ровно один раз, то каждая вершина должна иметь четную степень. Получим, что степень
любой вершины из
ровно один раз, то каждая вершина должна иметь четную степень. Получим, что степень
любой вершины из  должна быть либо четной, либо бесконечной.
должна быть либо четной, либо бесконечной. - Разобьем цепь
 на три подцепи
на три подцепи  так,
что
так,
что 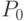 — конечная цепь, содержащая все ребра
графа
— конечная цепь, содержащая все ребра
графа  (и, быть может, другие ребра), а
(и, быть может, другие ребра), а 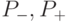 — две бесконечные в
одну сторону цепи. Тогда бесконечный граф
— две бесконечные в
одну сторону цепи. Тогда бесконечный граф  , образованный ребрами
цепей
, образованный ребрами
цепей 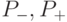 (а также инцидентными вершинами), имеет не
более двух бесконечных компонент. Так как
(а также инцидентными вершинами), имеет не
более двух бесконечных компонент. Так как  получается
из
получается
из  присоединением лишь конечного множества ребер, то отсюда и следует нужный результат.
присоединением лишь конечного множества ребер, то отсюда и следует нужный результат. - Пусть
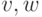 — начальная и конечная вершины
цепи
— начальная и конечная вершины
цепи 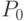 . Покажем, что
. Покажем, что 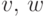 связаны в
связаны в  . Если
. Если 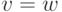 ,
то это очевидно. Если
,
то это очевидно. Если  , то применяя следствие ( связный граф является полуэйлеровым тогда и только тогда, если в нем не более двух вершин имеют нечетные степени)
к графу, полученному из
, то применяя следствие ( связный граф является полуэйлеровым тогда и только тогда, если в нем не более двух вершин имеют нечетные степени)
к графу, полученному из 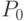 путем удаления ребер
графа
путем удаления ребер
графа  предполагаем , что в этом ( графе ровно две вершины, а именно
предполагаем , что в этом ( графе ровно две вершины, а именно 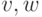 , имеют
нечетные степени), получим требуемый результат.
, имеют
нечетные степени), получим требуемый результат.
Можно получить соответствующие необходимые условия для полуэйлеровых бесконечных графов.
Теорема 6.4.
Пусть  — связный счетный граф, являющийся полуэйлеровым,
но не эйлеровым. Тогда:
— связный счетный граф, являющийся полуэйлеровым,
но не эйлеровым. Тогда:
-
 содержит либо не более одной вершины нечетной степени, либо
не менее одной вершины бесконечной степени.
содержит либо не более одной вершины нечетной степени, либо
не менее одной вершины бесконечной степени. - Для каждого конечного подграфа
 графа
графа  бесконечный граф
бесконечный граф 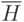 (описанный ранее) содержит ровно одну бесконечную
компоненту.
(описанный ранее) содержит ровно одну бесконечную
компоненту.
Оказывается, условие двух предыдущих теорем является не только необходимым, но и достаточным. Этот результат сформулируем в виде следующий теоремы, доказательство которой выходит за рамки данных лекций, его можно найти у Оре (Оре О., Теория графов, "Наука". М.: 1968).
Теорема 6.5.
Пусть  — связный счетный граф.
— связный счетный граф.  является
эйлеровым графом тогда и только тогда, когда выполнены следующие условия:
является
эйлеровым графом тогда и только тогда, когда выполнены следующие условия:
- В графе
 нет вершин нечетной степени;
нет вершин нечетной степени; - для каждого конечного подграфа
 графа
графа  бесконечный граф
бесконечный граф 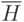 (полученный путем удаления из
(полученный путем удаления из  ребер
графа
ребер
графа  ) имеет не более двух бесконечных связных компонент;
) имеет не более двух бесконечных связных компонент; - если, кроме того, степень любой вершины из
 четна,
то
четна,
то 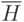 имеет ровно одну бесконечную связную компоненту.
имеет ровно одну бесконечную связную компоненту.
Более того,  является полуэйлеровым тогда и только
тогда, если выполнены либо эти условия, либо следующие условия:
является полуэйлеровым тогда и только
тогда, если выполнены либо эти условия, либо следующие условия:

