| Что такое сеть? |
Представления о планарном графе
Триангулированный граф
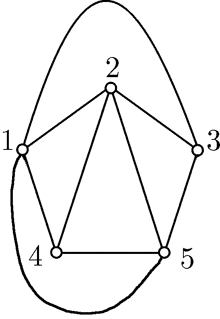
Рассмотрим плоский граф  с пятью вершинами.
с пятью вершинами.
Если добавить к нему ребра 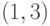 и
и  , то
полученный новый граф
, то
полученный новый граф  тоже будет плоским.
тоже будет плоским.
К этому графу не удается добавить ни одного ребра так, чтобы новый граф тоже был плоским.
Плоский граф называется максимально плоским, если невозможно добавить к нему ни одного ребра так, чтобы полученный граф был плоским. Изображенный граф является максимально плоским.
Каждая грань в плоском представлении максимально плоского графа
имеет  вершины. Поэтому максимально плоский граф
называют триангулированным.
вершины. Поэтому максимально плоский граф
называют триангулированным.
Операция добавления новых ребер, в результате которой в плоском представлении каждая грань имеет ровно 3 вершины, называется триангуляцией графа.
Задачи
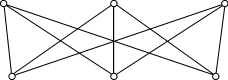
Задача 1. На участке три дома и три колодца. От каждого дома к каждому колодцу ведет тропинка.
Когда владельцы домов поссорились, они задумали проложить дороги от каждого дома к каждому колодцу так, чтобы не встречаться на пути к колодцам. Нужно показать, что их намерения не могут осуществиться.
Решение. Для решения задачи
достаточно доказать, что граф  ,
изображенный на рисунке, не плоский.
,
изображенный на рисунке, не плоский.
Предположим, что граф  — плоский, то есть существует
его плоское представление. Граф
— плоский, то есть существует
его плоское представление. Граф  — связный, он не имеет ни одного
моста, поэтому не имеет и перегородок. По формуле Эйлера,
— связный, он не имеет ни одного
моста, поэтому не имеет и перегородок. По формуле Эйлера, 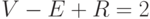 . Здесь
. Здесь  — число вершин,
— число вершин,  — число ребер,
— число ребер,  —
число граней с учетом бесконечной грани. Подсчитаем число вершин и ребер:
—
число граней с учетом бесконечной грани. Подсчитаем число вершин и ребер:  = 6,
= 6,  =
9, поэтому
=
9, поэтому 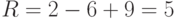 .
.
Теперь оценим удвоенное число ребер 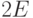 . Заметим, что в графе
нет простых циклов длиной 3, то есть граница любой грани в плоском
представлении графа
. Заметим, что в графе
нет простых циклов длиной 3, то есть граница любой грани в плоском
представлении графа  содержит не менее четырех ребер. Заметим,
что каждое ребро служит границей двух граней, так как мы учитываем и
бесконечную грань. При этом число
содержит не менее четырех ребер. Заметим,
что каждое ребро служит границей двух граней, так как мы учитываем и
бесконечную грань. При этом число 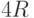 не может быть больше
удвоенного числа всех ребер:
не может быть больше
удвоенного числа всех ребер:  . Если бы мы знали число ребер в
границе каждой грани, то их сумма должна быть равна
. Если бы мы знали число ребер в
границе каждой грани, то их сумма должна быть равна 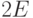 ; но
известно, что
; но
известно, что  , а
, а  , откуда
, откуда  . Полученное противоречие доказывает, что предположение было неверное, то есть граф
. Полученное противоречие доказывает, что предположение было неверное, то есть граф  — не плоский. Таким образом, намерения соседей неосуществимы.
— не плоский. Таким образом, намерения соседей неосуществимы.
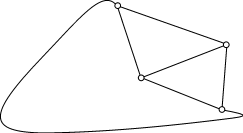
Задача 2. Каждый из четырех соседей соединил свой дом с тремя другими дорожками, которые пересекались лишь около домов.
Требуется доказать, что дом пятого соседа со всеми остальными домами соединить непересекающимися дорожками невозможно, то есть он вынужден построить мост или рыть подземный ход.
Решение. Решение задачи сводится
к доказательству того, что полный
граф  с пятью вершинами не является плоским.
с пятью вершинами не является плоским.
Предположим, что граф  плоский, то есть существует его
плоское представление. Граф
плоский, то есть существует его
плоское представление. Граф  — связный, он не имеет перегородок,
так как не имеет ни одного моста. Для плоского представления графа
— связный, он не имеет перегородок,
так как не имеет ни одного моста. Для плоского представления графа  верна
формула Эйлера. Подсчитаем число вершин и ребер:
верна
формула Эйлера. Подсчитаем число вершин и ребер: 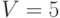 ,
,  , тогда
, тогда 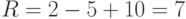 .
.
Оценим удвоенное число ребер 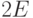 . Каждая грань ограничена не
более чем тремя ребрами (граф полный). Каждое ребро принадлежит границам двух
граней, поэтому число
. Каждая грань ограничена не
более чем тремя ребрами (граф полный). Каждое ребро принадлежит границам двух
граней, поэтому число 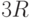 не может быть больше числа
не может быть больше числа 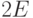 , то есть
, то есть  . Но
. Но  , а
, а  , то
есть
, то
есть 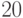 ,
, 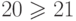 .
Противоречие доказывает, что предположение было неверным, то есть граф
.
Противоречие доказывает, что предположение было неверным, то есть граф  — не плоский.
— не плоский.