| Что такое сеть? |
Основные понятия теории графов
Задачи, приводящие к графам
Задача 1. Лист бумаги Плюшкин (Н.В.Гоголь "Мертвые души")
разрезает на три части. Некоторые из полученных листов он также разрезает
на три части. Несколько новых листков он вновь разрезает на три более
мелкие части и так далее. Сколько Плюшкин получает листиков бумаги, если
разрезает  листов?
листов?
Решение. Будем считать листы
бумаги вершинами графа. При разрезании
одного листка на три части число листков увеличивается на два (появляются
три новых вместо одного). Если же было разрезано  листов, то
образовалось
листов, то
образовалось 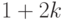 листов.
листов.
Задача 2. Утверждают, что в одной компании из пяти человек каждый знаком с двумя другими. Возможна ли такая компания?
Решение. Каждого из этой компании будем считать вершиной графа. Двое знакомых соединим ребром. Из рассматриваемой компании нельзя выделить ни "четырехугольник", ни "треугольник", поскольку тогда из оставшихся нельзя будет составить компанию, удовлетворяющую условию. То есть схема знакомства единственная. Всякую схему, напоминающую многоугольник, принято называть циклом. Древние греки "цикл" называли "колесом".
Задача 3. Девять шахматистов проводят турнир в один круг (каждый из участников должен сыграть с каждым по одному разу). Покажите, что в любой момент найдутся двое, закончившие одинаковое число партий.
Решение. Переведем условие задачи на язык графов. Каждому из шахматистов поставим в соответствие вершину графа, соединим ребрами попарно вершины, соответствующие шахматистам, уже сыгравшим партию друг с другом. Получим граф с девятью вершинами. Степени его вершин равняются числу партий, сыгравших с соответствующими игроками. Покажем, что во всяком графе с девятью вершинами всегда найдутся хотя бы две вершины одинаковой степени.
Каждая вершина графа с девятью вершинами может иметь степень, равную 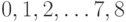 . Предположим, что существует
граф
. Предположим, что существует
граф 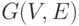 , все вершины которого имеют разную степень, т.е. каждое из чисел
последовательности
, все вершины которого имеют разную степень, т.е. каждое из чисел
последовательности 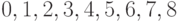 является степенью одной и
только одной из его вершин. Но этого не может быть. Действительно, если в графе
есть вершина
является степенью одной и
только одной из его вершин. Но этого не может быть. Действительно, если в графе
есть вершина  степени
степени  , то в нем не найдется
вершина
, то в нем не найдется
вершина  со степенью
со степенью  , так как эта вершина
, так как эта вершина  должна быть
соединена ребрами со всеми остальными вершинами графа, в том числе с
должна быть
соединена ребрами со всеми остальными вершинами графа, в том числе с  . Иначе говоря,
в графе с девятью вершинами не могут быть одновременно вершины степени
. Иначе говоря,
в графе с девятью вершинами не могут быть одновременно вершины степени  и
и  . Следовательно, найдутся хотя бы две вершины, степени которых
равны между собой. Таким образом, доказано, что в любой момент найдутся хотя бы
двое, сыгравшие одинаковое число партий.
. Следовательно, найдутся хотя бы две вершины, степени которых
равны между собой. Таким образом, доказано, что в любой момент найдутся хотя бы
двое, сыгравшие одинаковое число партий.
Вывод. Во всяком графе с  вершинами, где
вершинами, где  , всегда
найдутся по меньшей мере две вершины с одинаковыми степенями.
, всегда
найдутся по меньшей мере две вершины с одинаковыми степенями.
Задача 4. Девять человек проводят шахматный турнир в один круг. К некоторому моменту выясняется, что в точности двое сыграли одинаковое число партий. Нужно доказать, что либо в точности один участник еще не сыграл ни одной партии, либо в точности один сыграл все партии.
Решение. Переведем условие задачи
на язык графов. Пусть вершины
графа — игроки, а каждое ребро означает, что соответствующие игроки уже
сыграли между собой партию. Из условия известно, что в точности две
вершины имеют одинаковые степени. Требуется доказать, что в таком графе
всегда найдется либо только одна изолированная вершина, либо только одна
вершина степени  .
.
В общем случае у графа с девятью вершинами степень каждой вершины может
принимать одно из девяти значений: 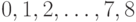 . Но у
такого графа степени вершин принимают только восемь разных значений, ибо ровно
две вершины имеют одинаковую степень. Следовательно, обязательно
либо
. Но у
такого графа степени вершин принимают только восемь разных значений, ибо ровно
две вершины имеют одинаковую степень. Следовательно, обязательно
либо  , либо
, либо  будет значением степени одной из вершин.
будет значением степени одной из вершин.
Докажем, что в графах с девятью вершинами, из которых в точности две имеют
одинаковую степень, не может быть двух вершин степени  или двух
вершин степени
или двух
вершин степени  .
.
Допустим, что все же найдется граф с девятью вершинами, в котором ровно две вершины изолированные, а все остальные имеют разные степени. Тогда, если не рассматривать эти две изолированные вершины, останется граф с семью вершинами, степени которых не совпадут. Но такого графа не существует (см. задачу 3). Значит, это предположение неверно.
Теперь допустим, что существует граф с девятью вершинами, в котором ровно
две вершины имеют степень  , а все остальные —
несовпадающие степени.
Тогда в дополнении данного графа ровно две вершины будут иметь
степень
, а все остальные —
несовпадающие степени.
Тогда в дополнении данного графа ровно две вершины будут иметь
степень  , а остальные — попарно различные степени. Этого
тоже не может быть (см. задачу 3), то есть и второе предположение
неверно.
, а остальные — попарно различные степени. Этого
тоже не может быть (см. задачу 3), то есть и второе предположение
неверно.
Следовательно, у графа с девятью вершинами, из которых в точности две
имеют одинаковую степень, всегда найдется либо одна изолированная вершина,
либо одна вершина степени  .
.
Вернемся к задаче. Как и требовалось доказать, среди рассмотренных девяти
игроков либо только один еще не сыграл ни одной партии, либо только один
сыграл все партии. При решении этой задачи число 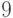 можно заменить
любым другим натуральным числом
можно заменить
любым другим натуральным числом 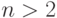 .
.
Вывод. Если в графе с  вершинами
вершинами 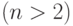 в точности две вершины
имеют одинаковую степень, то в этом графе всегда найдется либо в точности
одна вершина степени
в точности две вершины
имеют одинаковую степень, то в этом графе всегда найдется либо в точности
одна вершина степени  , либо в точности одна вершина
степени
, либо в точности одна вершина
степени  .
.

