| Россия, Санкт-Петербург |
Последовательности (деревья)
Представления
Почти все машинные представления деревьев основаны на связанных
распределениях. Каждый узел состоит из поля  и нескольких
полей для
указателей. Например, представление, которое будет удобным для изложения
множества и мультимножества, для каждого узла имеет единственное поле для
указателя
и нескольких
полей для
указателей. Например, представление, которое будет удобным для изложения
множества и мультимножества, для каждого узла имеет единственное поле для
указателя  , указывающего на отца данного узла. При этом
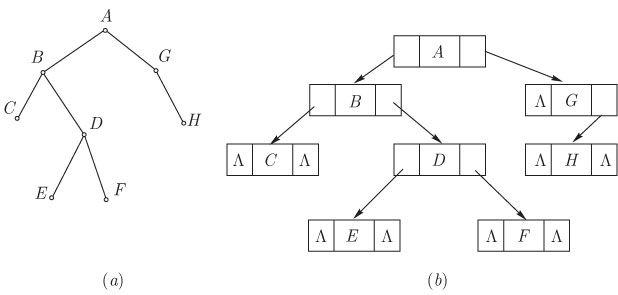
приведенное на рис. 4.1 дерево будет выглядеть так,
как показано на рис. 4.5.
Такое представление полезно, если необходимо подниматься по дереву от
потомков к предкам. Такая операция встречается довольно редко. Чаще требуется
опуститься по дереву от предков к потомкам.
, указывающего на отца данного узла. При этом
приведенное на рис. 4.1 дерево будет выглядеть так,
как показано на рис. 4.5.
Такое представление полезно, если необходимо подниматься по дереву от
потомков к предкам. Такая операция встречается довольно редко. Чаще требуется
опуститься по дереву от предков к потомкам.
Представление дерева (или леса) с использованием указателей, ведущих от предков к потомкам, довольно сложно, поскольку узел, имея не более чем одного отца, может в то же время иметь произвольно много сыновей. Другими словами, при таком представлении узлы должны различаться по размеру, что является определенным неудобством. Один из путей обхода этой трудности состоит в том, чтобы определить соответствие между деревьями и бинарными деревьями, поскольку бинарные деревья легко представить узлами фиксированного размера.
Каждый узел в этом случае имеет три поля: 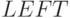 , указатель
местоположения корня левого поддерева,
, указатель
местоположения корня левого поддерева,  , содержимое узла,
и
, содержимое узла,
и 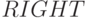 , указатель местоположения
корня правого поддерева. Все сказанное выше проиллюстрировано на рис. 4.6.
, указатель местоположения
корня правого поддерева. Все сказанное выше проиллюстрировано на рис. 4.6.
Можно представлять деревья как бинарные, используя узлы фиксированного
размера, представляя каждый узел леса в виде узла, состоящего из полей 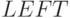 ,
,  ,
, 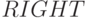 . При этом
. При этом 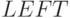 предназначается для указания самого левого
сына данного узла, а поле
предназначается для указания самого левого
сына данного узла, а поле 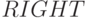 - для указания следующего брата
данного дочернего/сыновнего узла.
- для указания следующего брата
данного дочернего/сыновнего узла.
Прохождения
Во многих приложениях необходимо пройти лес, заходя в узлы, то есть обрабатывая их некоторым систематическим образом. Посещение каждого узла может быть связано с простой операцией, такой как печать содержимого, или со сложной, такой как вычисление функции. Будем предполагать, что при посещении узла структура леса не меняется. Рассмотрим четыре основных способа прохождения леса: в глубину, снизу вверх, в горизонтальном порядке и для бинарных деревьев - в симметричном порядке.
При прохождении в глубину, известном также как прохождение в прямом порядке, узлы леса проходятся в соответствии со следующей рекурсивной процедурой:
- Посетить корень первого дерева.
- пройти в глубину поддерева первого дерева (если оно есть).
- Пройти в глубину оставшиеся деревья, если они есть.
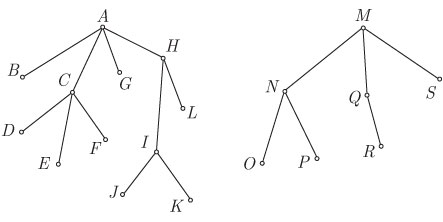
Например, для леса, показанного на рис. 4.7, узлы будут проходиться в
следующем
порядке: 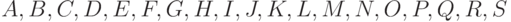 .
.
Название "в глубину" отражает тот факт, что после посещения некоторого узла мы продолжаем прохождение в глубь дерева всякий раз, когда это возможно. Такой порядок особенно полезен в процедурах поиска.
Для бинарных деревьев эта процедура упрощается и выглядит следующим образом.
- Посетить корень.
- Пройти в глубину левое поддерево
- Пройти в глубину правое поддерево.
Прохождение снизу вверх, известное также как обратный порядок или концевой порядок, осуществляется согласно следующей рекурсивной процедуре:
- Пройти снизу вверх поддеревья первого дерева, если они есть.
- Посетить корень первого дерева.
- Пройти снизу вверх оставшиеся деревья, если они есть.
Название "снизу вверх" связано с тем, что в момент посещения
произвольного узла
его потомки оказываются уже пройденными. Такой порядок прохождения полезен, в
частности, потому, что он позволяет вычислять рекурсивно определенные функции
на
лесах. При этом порядке прохождения узлы леса, показанного на
рис. 4.7,
проходятся в такой последовательности: 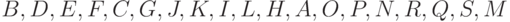 .
Рекурсивная
процедура прохождения снизу вверх применительно к бинарным деревьям имеет
следующий вид:
.
Рекурсивная
процедура прохождения снизу вверх применительно к бинарным деревьям имеет
следующий вид:
- Пройти снизу вверх левое дерево.
- Пройти снизу вверх правое дерево.
- Посетить корень.
Симметричный порядок для бинарных деревьев определяется рекурсивно следующим образом:
- Пройти в симметричном порядке левое поддерево.
- Посетить корень.
- Пройти в симметричном порядке правое поддерево.
Такой способ прохождения известен также как лексикографический порядок или внутренний порядок. Заметим, что прохождение леса снизу вверх эквивалентно прохождению в симметричном порядке бинарного дерева, соответствующего этому лесу (при естественном соответствии).
Сравнивая рекурсивные процедуры прохождения бинарных деревьев в глубину, снизу вверх и в симметричном порядке, можно обнаружить их значительное сходство:
Это сходство позволяет построить общий нерекурсивный алгоритм, который может быть применен к каждому из этих порядков прохождения бинарных деревьев.
Горизонтальный
порядок прохождения. При таком способе узлы леса
проходятся слева направо, уровень за уровнем от корня вниз. Таким образом, в
соответствии с этой процедурой узлы леса, показанного на рис.4.7, будут
проходиться в следующем порядке: 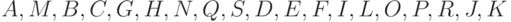 .
Такое прохождение дерева полезно в определенных алгоритмах на графах.
.
Такое прохождение дерева полезно в определенных алгоритмах на графах.