| Россия, Санкт-Петербург |
Последовательности (множества и мультимножества)
Множества и мультимножества
Не существует формального определения множества ; считается что это понятие первичное и не определяется. Так, можно говорить, что множество есть объединение различных элементов, но при этом мы оставляем неопределяемыми понятия "объединение" и "элементы". Дадим следующее определение множеству: множество - это неупорядоченная совокупность различных объектов или структура данных, используемая для представления множества. Мультимножество есть объединение не обязательно различных элементов; его можно считать множеством, в котором каждому элементу поставлено в соответствие положительное целое число, называемое кратностью.
Конечное множество  будем записывать в следующем виде:
будем записывать в следующем виде:
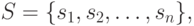
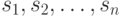 - элементы
- элементы  , обязательно различные!
Мощность множества
, обязательно различные!
Мощность множества  обозначается как
обозначается как 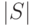 ,
для выписанного выше множества мощность записывается так
,
для выписанного выше множества мощность записывается так 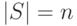 . Если
. Если  - конечное
мультимножество, то будем записывать его в следующем виде:
- конечное
мультимножество, то будем записывать его в следующем виде:
 различны и
различны и  - кратность элемента
- кратность элемента  . В этом случае мощность
. В этом случае мощность  равна
равна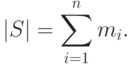
 и
и  , а для мультимножеств -
, а для мультимножеств - 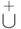 и
и 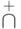 .
Последовательное и связанное представление последовательностей можно
использовать для множеств и мультимножеств очевидным способом. Индуцируя
искусственный порядок элементов множества или используя собственный порядок,
если он существует, можно рассматривать множество как последовательность.
Аналогично, как последовательность можно рассматривать и мультимножество, или,
для того чтобы сэкономить место, его можно рассматривать как последовательность
пар, каждая из которых состоит из элемента и его кратности.
.
Последовательное и связанное представление последовательностей можно
использовать для множеств и мультимножеств очевидным способом. Индуцируя
искусственный порядок элементов множества или используя собственный порядок,
если он существует, можно рассматривать множество как последовательность.
Аналогично, как последовательность можно рассматривать и мультимножество, или,
для того чтобы сэкономить место, его можно рассматривать как последовательность
пар, каждая из которых состоит из элемента и его кратности.Как и для последовательностей, наилучший метод представления множеств или
мультимножеств существенно зависит от операций, которые выполняются над ними.
Предположим, например, что имеем дело с непересекающимися подмножествами
множества 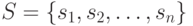 и что над ними необходимо
выполнить две следующие операции: объединение двух
множеств и отыскание подмножества, содержащего данное
и что над ними необходимо
выполнить две следующие операции: объединение двух
множеств и отыскание подмножества, содержащего данное  . Таким
образом, в любой момент времени имеем разбиение
. Таким
образом, в любой момент времени имеем разбиение  на непустые
непересекающиеся подмножества. Рассмотрим эти операции в конце
данной лекции.
на непустые
непересекающиеся подмножества. Рассмотрим эти операции в конце
данной лекции.
С целью идентификации считаем, что каждое из непересекающихся
подмножеств множества  имеет имя. Имя - это просто один из элементов подмножества,
или, иначе, - представитель подмножества. Когда мы будем ссылаться на имя подмножества, то
будем под этим подразумевать его представителя. Рассмотрим, например,
множество
имеет имя. Имя - это просто один из элементов подмножества,
или, иначе, - представитель подмножества. Когда мы будем ссылаться на имя подмножества, то
будем под этим подразумевать его представителя. Рассмотрим, например,
множество

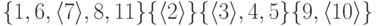 |
( 6.1) |
 следующего вида:
следующего вида: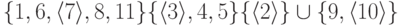
Именем множества 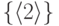

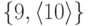 может быть или 2, или 10.Предполагаем,
что вначале имеется разбиение множества
может быть или 2, или 10.Предполагаем,
что вначале имеется разбиение множества  на
на  подмножеств, каждое из которых состоит из одного элемента
подмножеств, каждое из которых состоит из одного элемента
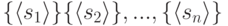 |
( 6.2) |
Для реализации операций и объединения, и отыскания опишем процедуры
(операции)  и
и  . Процедура
(операция)
. Процедура
(операция)  по именам двух различных подмножеств
по именам двух различных подмножеств  и
и  образует новое подмножество, содержащее все элементы множеств
образует новое подмножество, содержащее все элементы множеств  и
и  . Процедура (операция)
. Процедура (операция) 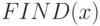 выдает имя множества, содержащего
выдает имя множества, содержащего  . Например, если нужно
множество,содержащее
. Например, если нужно
множество,содержащее  , объединить с множеством, содержащим
, объединить с множеством, содержащим  ,
необходимо выполнить следующую последовательность операторов:
,
необходимо выполнить следующую последовательность операторов:
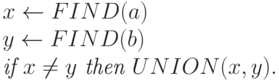
Предположим, что мы имеем  операций объединения, перемешанных
с
операций объединения, перемешанных
с  операциями отыскания, и что начинаем алгоритм с множества
операциями отыскания, и что начинаем алгоритм с множества 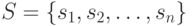 , которое разбито на подмножества, состоящие из одного
элемента (см. 6.2.). Найдем такую структуру данных для представления
непересекающихся подмножеств множества
, которое разбито на подмножества, состоящие из одного
элемента (см. 6.2.). Найдем такую структуру данных для представления
непересекающихся подмножеств множества  , чтобы последовательность
операций можно было производить эффектно. Такой структурой данных
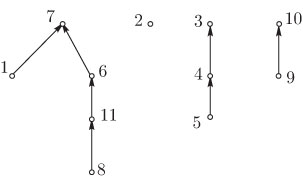
является представление в виде леса с указателями отца, как показано на
рис. 4.5 лекции 4. Каждый элемент
, чтобы последовательность
операций можно было производить эффектно. Такой структурой данных
является представление в виде леса с указателями отца, как показано на
рис. 4.5 лекции 4. Каждый элемент  множества будет узлом
леса, а отцом его будет элемент из того же подмножества, что и
множества будет узлом
леса, а отцом его будет элемент из того же подмножества, что и  . Если
элемент не имеет отца, то есть является корнем, то он будет именем своего
подмножества. В соответствии с этим разбиение 6.1 может быть представлено
так:
. Если
элемент не имеет отца, то есть является корнем, то он будет именем своего
подмножества. В соответствии с этим разбиение 6.1 может быть представлено
так:
При таком представлении процедура (операция) 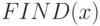 состоит в
переходах по указателям отцов от
состоит в
переходах по указателям отцов от  до корня, то есть имени, его
подмножества. Процедура (операция)
до корня, то есть имени, его
подмножества. Процедура (операция)  состоит в
связывании вместе некоторым образом деревьев, имеющих корни
состоит в
связывании вместе некоторым образом деревьев, имеющих корни  и
и  . Например, такую связь можно осуществить, сделав
. Например, такую связь можно осуществить, сделав  отцом
отцом  .
.
После  операций объединения наибольшее из возможных
подмножеств, получающихся в результате разбиения
операций объединения наибольшее из возможных
подмножеств, получающихся в результате разбиения  , будет содержать
, будет содержать 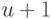 элементов. Поскольку каждое объединение уменьшает число подмножеств на
единицу, последовательность операций может содержать не более
элементов. Поскольку каждое объединение уменьшает число подмножеств на
единицу, последовательность операций может содержать не более  объединений, откуда
объединений, откуда 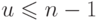 . Так как каждая операция
объединения изменяет имя подмножества, содержащего
некоторые элементы, можно считать, что каждому объединению предшествует по
крайней мере одно отыскание, в связи с чем естественно предположить, что
. Так как каждая операция
объединения изменяет имя подмножества, содержащего
некоторые элементы, можно считать, что каждому объединению предшествует по
крайней мере одно отыскание, в связи с чем естественно предположить, что 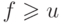 . Выясним, насколько эффективно можно выполнить
последовательность из
. Выясним, насколько эффективно можно выполнить
последовательность из 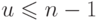 операций объединения,
перемешанных с
операций объединения,
перемешанных с 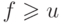 операциями отыскания. Время,
требуемое на операции объединения, очевидно, пропорционально
операциями отыскания. Время,
требуемое на операции объединения, очевидно, пропорционально  , потому
что необходимая для каждой операции объединения переделка некоторых
указателей требует фиксированного количества работы. Поэтому сосредоточим свое
внимание на времени, требуемом для
, потому
что необходимая для каждой операции объединения переделка некоторых
указателей требует фиксированного количества работы. Поэтому сосредоточим свое
внимание на времени, требуемом для  операций отыскания.
операций отыскания.
Если операция  выполняется путем назначения
выполняется путем назначения  отцом
отцом  , то после
, то после  операций
объединения может получиться лес, показанный ниже.
операций
объединения может получиться лес, показанный ниже.

В этом случае, если  операций отыскания
выполняются после всех операций объединения и каждый поиск начинается
внизу цепи из
операций отыскания
выполняются после всех операций объединения и каждый поиск начинается
внизу цепи из 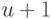 элементов множества, то ясно, что время,
требуемое на операции отыскания, будет пропорционально
элементов множества, то ясно, что время,
требуемое на операции отыскания, будет пропорционально 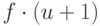 .
Очевидно, оно не может быть больше, чем константа, умноженная на
.
Очевидно, оно не может быть больше, чем константа, умноженная на 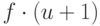 . Можно существенно уменьшить эту оценку.
. Можно существенно уменьшить эту оценку.
Формула включений и исключений
Пусть имеется  предметов, некоторые из которых обладают
свойствами
предметов, некоторые из которых обладают
свойствами 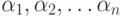 . При этом каждый предмет
может либо не обладать ни одним из этих свойств, либо обладать одним или несколькими
свойствами. Обозначим через
. При этом каждый предмет
может либо не обладать ни одним из этих свойств, либо обладать одним или несколькими
свойствами. Обозначим через  количество предметов, обладающих свойствами
количество предметов, обладающих свойствами 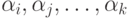 (и быть может, еще некоторыми из других свойств).
Если нужно взять предметы, не обладающие некоторым свойством, то эти свойства
пишем со штрихом. Например, через
(и быть может, еще некоторыми из других свойств).
Если нужно взять предметы, не обладающие некоторым свойством, то эти свойства
пишем со штрихом. Например, через  ) обозначено количество предметов, обладающих свойствами
) обозначено количество предметов, обладающих свойствами 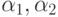 , но не обладающих свойством
, но не обладающих свойством 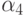 (вопрос об
остальных свойствах останется открытым). Число предметов, не обладающих ни одним из указанных свойств,
обозначается по этому правилу через
(вопрос об
остальных свойствах останется открытым). Число предметов, не обладающих ни одним из указанных свойств,
обозначается по этому правилу через 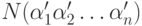 . Общий закон состоит в том, что
. Общий закон состоит в том, что
 |
( 6.3) |
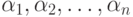 (без учета их порядка),
причем знак + ставится, если число учитываемых свойств четно, и знак
(без учета их порядка),
причем знак + ставится, если число учитываемых свойств четно, и знак  , если
это число нечетно. Например,
, если
это число нечетно. Например, 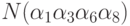 входит со знаком +, а
входит со знаком +, а 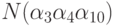 со знаком
со знаком 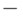 . Формулу 6.3 называют формулой включений и исключений -
сначала исключаются все предметы, обладающие хотя бы одним из свойств
. Формулу 6.3 называют формулой включений и исключений -
сначала исключаются все предметы, обладающие хотя бы одним из свойств 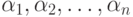 , потом включаются предметы,
обладающие, по крайней мере, двумя из этих свойств, затем исключаются
имеющие, по крайней мере, три и т.д.
, потом включаются предметы,
обладающие, по крайней мере, двумя из этих свойств, затем исключаются
имеющие, по крайней мере, три и т.д.