Последовательности (деревья)

Деревья

Конечное корневое дерево формально определяется как непустое множество упорядоченных узлов, таких, что существует один выделенный узел, называемый корнем дерева, а оставшиеся узлы разбиты на 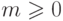поддеревьев 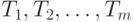. Будем рассматривать только корневые деревья. Узлы, не имеющие поддеревьев, называются листьями ; остальные узлы называются внутренними узлами.

Рис. 4.1.

В первой лекции уже было использовано дерево - при изучении необходимого числа взвешиваний в задаче о фальшивой монете с монетами. Так "рано" деревья появились в тексте не случайно, поскольку понятие дерева используется в различных важных аспектах данного курса. Посредством деревьев изображаются иерархические организации, поэтому они являются наиболее важными нелинейными структурами в комбинаторных алгоритмах.

В описании соотношений между узлами дерева используем терминологию, принятую в генеалогических деревьях. Так, говорят, что в дереве или поддереве все узлы являются потомками его корня, и наоборот, корень есть предок всех своих потомков. Корень именуют отцом корней его поддеревьев, которые в свою очередь будут сыновьями корня. Например, на рис. 4.1 узел является отцом узлов 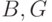и ; 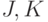- сыновья , а 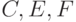- братья.

Все рассматриваемые нами деревья будут упорядочены, то есть для них будет важен относительный порядок поддеревьев каждого узла. Таким образом, деревья считаются различными.

Рис. 4.2. Различные деревья

Определим лес как упорядоченное множество деревьев; в связи с этим можно перефразировать определение дерева: дерево есть непустое множество узлов, такое, что существует один выделенный узел, называемый корнем дерева, а оставшиеся узлы образуют лес с 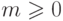поддеревьями корня. Важной разновидностью корневых деревьев является класс бинарных деревьев. Бинарное дерево либо пустое, либо состоит из выделенного узла, называемого корнем, и двух бинарных поддеревьев: левого 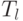и правого 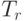. Бинарные деревья не являются подмножеством множества деревьев, они полностью отличаются по своей структуре, поскольку два следующих рисунка не изображают одно и то же бинарное дерево.

Рис. 4.3. Различные бинарные деревья

Как деревья, однако, они не отличаются от дерева, изображенного на рис. 4.4.

Рис. 4.4. Не бинарное дерево

Различие между деревом и бинарным деревом состоит в том, что дерево не может быть пустым, а каждый узел дерева может иметь произвольное число поддеревьев; в то же время, бинарное дерево может быть пустым. Каждая из вершин бинарного дерева может иметь 0, 1 или 2 поддерева, и существует различие между левым и правым поддеревьями.