| Россия, Санкт-Петербург |
Что такое граф? Определения и примеры
Введение
Множество самых разнообразных задач естественно формулируется в терминах графов. Так, например, могут быть сформулированы задачи составления расписаний в исследовании операций, анализа сетей в электротехнике, установления структуры молекул в органической химии, сегментации программ в программировании, анализа цепей Маркова в теории вероятностей. В задачах, возникающих в реальной жизни, соответствующие графы часто оказываются так велики, что их анализ неосуществим без ЭВМ. Таким образом, решение прикладных задач с использованием теории графов возможно в той мере, в какой возможна обработка больших графов на ЭВМ, и поэтому эффективные алгоритмы решения задач теории графов имеют большое практическое значение. В "Алгоритмы на графах" и "Калейдоскоп из комбинаторных алгоритмов" лекциях мы излагаем несколько эффективных алгоритмов на графах и используем их для демонстрации некоторой общей техники решения задач на графах с помощью ЭВМ.
Конечный граф 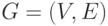 состоит из конечного множества вершин
состоит из конечного множества вершин 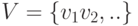 и конечного множества ребер
и конечного множества ребер 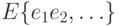 . Каждому ребру соответствует пара вершин: если ребро
. Каждому ребру соответствует пара вершин: если ребро 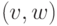 соответствует ребру
соответствует ребру  , то говорят, что
, то говорят, что  инцидентно вершинам
инцидентно вершинам  и
и  . Граф
. Граф  изображается следующим образом: каждая вершина
представляется точкой и каждое ребро представляется отрезком линии, соединяющим его
концевые вершины. Граф
называется ориентированным, если
пара вершин
изображается следующим образом: каждая вершина
представляется точкой и каждое ребро представляется отрезком линии, соединяющим его
концевые вершины. Граф
называется ориентированным, если
пара вершин 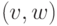 , соответствующая каждому ребру, упорядочена. В
таком случае говорят, что ребро
, соответствующая каждому ребру, упорядочена. В
таком случае говорят, что ребро  ориентированно
из вершины
ориентированно
из вершины  в вершину
в вершину  , а направление обозначается стрелкой
на ребре. Мы будем называть ориентированные графы орграфами. В неориентированном графе концевые вершины каждого ребра не упорядочены, и ребра не имеют направления. Ребро называется петлей, если оно начинается и кончается в одной и той же вершине.
Говорят, что два ребра
параллельны, если они имеют одну и ту же пару концевых вершин (и
если они имеют одинаковую ориентацию в случая ориентированного графа). Граф называется простым, если он не имеет ни петель,
ни параллельных ребер. Если не указывается противное, будем считать, что
рассматриваемые графы являются простыми. Всюду в
"Алгоритмы на графах"
и
"Калейдоскоп из комбинаторных алгоритмов"
лекции будем
использовать символы
, а направление обозначается стрелкой
на ребре. Мы будем называть ориентированные графы орграфами. В неориентированном графе концевые вершины каждого ребра не упорядочены, и ребра не имеют направления. Ребро называется петлей, если оно начинается и кончается в одной и той же вершине.
Говорят, что два ребра
параллельны, если они имеют одну и ту же пару концевых вершин (и
если они имеют одинаковую ориентацию в случая ориентированного графа). Граф называется простым, если он не имеет ни петель,
ни параллельных ребер. Если не указывается противное, будем считать, что
рассматриваемые графы являются простыми. Всюду в
"Алгоритмы на графах"
и
"Калейдоскоп из комбинаторных алгоритмов"
лекции будем
использовать символы  и
и 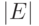 для обозначения соответственно числа вершин и числа ребер в графе
для обозначения соответственно числа вершин и числа ребер в графе 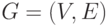 .
.
Представления
Наиболее известный способ представления графа на бумаге состоит в геометрическом изображении точек и линий. В ЭВМ граф должен быть представлен дискретным способом, причем возможно много различных представлений. Простота использования, так же как и эффективность алгоритмов на графе, зависит от подходящего выбора представления графа. Рассмотрим различные структуры данных для представления графов.
Матрица
смежностей. Одним из наиболее распространенных
машинных представлений простого графа является матрица смежностей или соединений. Матрица смежностей графа  есть
есть  -матрица
-матрица ![A = [a_{ij} ]](/sites/default/files/tex_cache/016a70c7f50215390f687535ab4072a2.png) , в
которой
, в
которой 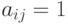 , если в
, если в  существует ребро, идущее из
существует ребро, идущее из  -й вершины в
-й вершины в  -ю, и
-ю, и 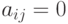 в противном случае. Орграф и его
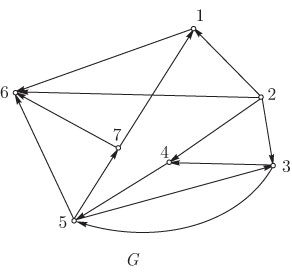
матрица смежностей представлены на рис. 12.1.
в противном случае. Орграф и его
матрица смежностей представлены на рис. 12.1.
![\left[ {\begin{array}{*{20}c}
0 & 0 & 0 & 0 & 0 & 1 & 0 \\
1 & 0 & 1 & 1 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 1 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 1 & 0
\end{array} } \right]](/sites/default/files/tex_cache/befd297291977cae1ee07822641b3a3b.png)
Заметим, что в матрице смежностей петля может быть представлена соответствующим единичным диагональным элементом. Кратные ребра можно представить, позволив элементу матрицы быть больше 1, но это не принято, так как обычно удобно представлять каждый элемент матрицы одним двоичным разрядом.
Для задания матрицы смежностей требуется 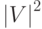 двоичных разрядов. У неориентированного графа матрица смежностей симметрична, и
для ее представления достаточно хранить только верхний треугольник. В
результате экономится почти 50% памяти, но время вычислений может при этом немного
увеличиться, потому что каждое обращение к
двоичных разрядов. У неориентированного графа матрица смежностей симметрична, и
для ее представления достаточно хранить только верхний треугольник. В
результате экономится почти 50% памяти, но время вычислений может при этом немного
увеличиться, потому что каждое обращение к  должно быть
заменено следующим: if
должно быть
заменено следующим: if 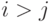 then
then 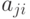 else
else  .
В случае представления графа его матрицей смежностей для большинства алгоритмов
требуется время вычисления, по крайней мере пропорциональное
.
В случае представления графа его матрицей смежностей для большинства алгоритмов
требуется время вычисления, по крайней мере пропорциональное 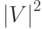 .
.
Матрица весов. Граф,
в котором ребру  сопоставлено число
сопоставлено число 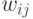 ,
называется взвешенным
графом, а число
,
называется взвешенным
графом, а число 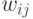 называется весом ребра
называется весом ребра  . В сетях связи
или транспортных сетях эти веса представляют некоторые физические
величины, такие как стоимость, расстояние, эффективность, емкость или
надежность соответствующего ребра. Простой взвешенный граф может быть представлен своей
матрицей весов
. В сетях связи
или транспортных сетях эти веса представляют некоторые физические
величины, такие как стоимость, расстояние, эффективность, емкость или
надежность соответствующего ребра. Простой взвешенный граф может быть представлен своей
матрицей весов ![W = \left[ {w_{ij} } \right]](/sites/default/files/tex_cache/46f891568eb36b2a8397c5edb3f48425.png) ,
где
,
где 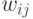 есть вес ребра, соединяющего вершины
есть вес ребра, соединяющего вершины  и
и  .
Веса несуществующих ребер обычно полагают равными
.
Веса несуществующих ребер обычно полагают равными  или 0 в зависимости от приложений. Когда
вес несуществующего ребра равен 0, матрица весов является простым обобщением матрицы смежностей.
или 0 в зависимости от приложений. Когда
вес несуществующего ребра равен 0, матрица весов является простым обобщением матрицы смежностей.
Список ребер. Если
граф является разреженным, то возможно, что более
эффектно представлять ребра графа парами вершин. Это представление можно
реализовать двумя массивами 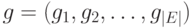 и
и 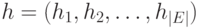 . Каждый
элемент в массиве есть метка вершины, а
. Каждый
элемент в массиве есть метка вершины, а  -е ребро графа выходит из
вершины
-е ребро графа выходит из
вершины  и входит в вершину
и входит в вершину  . Например, орграф,
изображенный на рис. 12.1, будет представляться следующим
образом:
. Например, орграф,
изображенный на рис. 12.1, будет представляться следующим
образом:
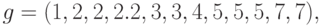
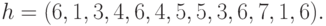
Структура смежности.
В ориентированном графе вершина  называется последователем другой
вершины
называется последователем другой
вершины  , если существует ребро, направленное
из
, если существует ребро, направленное
из  в
в  . Вершина
. Вершина  называется тогда предшественником
называется тогда предшественником  . В случае неориентированного графа две вершины называются соседями,
если между ними есть ребро. Граф может быть описан его структурой смежности, то
есть списком всех последователей (соседей) каждой вершины; для каждой
вершины
. В случае неориентированного графа две вершины называются соседями,
если между ними есть ребро. Граф может быть описан его структурой смежности, то
есть списком всех последователей (соседей) каждой вершины; для каждой
вершины  задается
задается  - список всех последователей
(соседей) вершины
- список всех последователей
(соседей) вершины  . В большинстве алгоритмов на графах
относительный порядок вершин, смежных с вершиной
. В большинстве алгоритмов на графах
относительный порядок вершин, смежных с вершиной  в
в  ,
не важен, и в таком случае удобно считать
,
не важен, и в таком случае удобно считать  мультимножеством (или множеством,
если граф является простым) вершин, смежных
с
мультимножеством (или множеством,
если граф является простым) вершин, смежных
с  . Структура смежности орграфа, представленного на рис. 12.1,
такова:
. Структура смежности орграфа, представленного на рис. 12.1,
такова:
Adj(v) 1: 6 2: 1, 3, 4, 6 3: 4, 5 4: 5 5: 3, 6, 7 6: 7: 1, 6
Если для хранения метки вершины используется одно машинное слово, то
структура смежности ориентированного графа требует 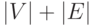 слов. Если граф неориентированный, нужно
слов. Если граф неориентированный, нужно  слов, так как каждое ребро встречается дважды.
слов, так как каждое ребро встречается дважды.
Структуры смежности могут быть удобно реализованы массивом из  линейно связанных списков, где каждый список содержит
последователей некоторой вершины. Поле данных содержит метку одного из последователей, и поле указателей
указывает следующего последователя. Хранение списков смежности в виде
связанного списка желательно для алгоритмов, в которых в графе добавляются или удаляются вершины.
линейно связанных списков, где каждый список содержит
последователей некоторой вершины. Поле данных содержит метку одного из последователей, и поле указателей
указывает следующего последователя. Хранение списков смежности в виде
связанного списка желательно для алгоритмов, в которых в графе добавляются или удаляются вершины.
Матрица инцидентности -  задает граф :
задает граф : 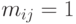 ,
если ребро
,
если ребро  выходит из вершины
выходит из вершины  ,
,  ,
если ребро
,
если ребро  входит в вершину
входит в вершину  , и
, и 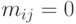 в остальных случаях.
в остальных случаях.
Связность и расстояние
Говорят, что вершины  и
и  в графе смежны,
если существует ребро, соединяющее их.
Говорят, что два ребра смежны, если они
имеют общую вершину. Простой
путь, или для краткости, просто путь,
записываемый иногда как
в графе смежны,
если существует ребро, соединяющее их.
Говорят, что два ребра смежны, если они
имеют общую вершину. Простой
путь, или для краткости, просто путь,
записываемый иногда как 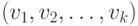 , - это
последовательность смежных ребер
, - это
последовательность смежных ребер 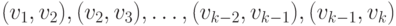 , в которой все
вершины
, в которой все
вершины 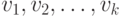 различны, исключая, возможно,
случай
различны, исключая, возможно,
случай  . В орграфе этот путь называется ориентированным
из
. В орграфе этот путь называется ориентированным
из 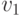 в
в  , в неориентированном графе он называется
путем между
, в неориентированном графе он называется
путем между 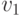 и
и  . Число ребер в пути называется длиной пути. Путь наименьшей длины
называется кратчайшим
путем. Замкнутый путь называется циклом.
Граф, который не содержит циклов, называется ациклическим.
. Число ребер в пути называется длиной пути. Путь наименьшей длины
называется кратчайшим
путем. Замкнутый путь называется циклом.
Граф, который не содержит циклов, называется ациклическим.
Подграф графа  есть граф, вершины и ребра которого
лежат в
есть граф, вершины и ребра которого
лежат в  . Подграф
. Подграф  , индуцированный
подмножеством
, индуцированный
подмножеством  множества
множества  вершин
графа
вершин
графа  , - это подграф, который получается в результате удаления
всех вершин из
, - это подграф, который получается в результате удаления
всех вершин из  и всех ребер, инцидентных им.
и всех ребер, инцидентных им.
Неориентированный
граф  связен,
если существует хотя бы один путь в
связен,
если существует хотя бы один путь в  между
каждой парой вершин
между
каждой парой вершин 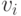 и
и 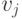 . Ориентированный граф
. Ориентированный граф  связен,
если неориентированный граф, получающийся
из
связен,
если неориентированный граф, получающийся
из  путем удаления ориентации ребер, является связным. Граф, состоящий из
единственной изолированной вершины, является (тривиально) связным.
Максимальный связный подграф графа
путем удаления ориентации ребер, является связным. Граф, состоящий из
единственной изолированной вершины, является (тривиально) связным.
Максимальный связный подграф графа  называется связной компонентой или просто компонентой
называется связной компонентой или просто компонентой  . Несвязный граф состоит из двух или более компонент.
Максимальный сильно связный подграф называется сильно связной компонентой.
. Несвязный граф состоит из двух или более компонент.
Максимальный сильно связный подграф называется сильно связной компонентой.
Иногда недостаточно знать, что граф связен; нас может интересовать, насколько "сильно связен" связный граф. Например, связный граф может содержать вершину, удаление которой вместе с инцидентными ей ребрами разъединяет оставшиеся вершины. Такая вершина называется точкой сочленения или разделяющей вершиной. Граф, содержащий точку сочленения, называется разделимым. Граф без точек сочленения называется двусвязным или неразделимым. Максимальный двусвязный подграф графа называется двусвязной компонентой или блоком.
Большинство основных вопросов о графах касается связности, путей и расстояний. Нас может интересовать вопрос, является ли граф связным; если он связен, то может оказаться нужным найти кратчайшее расстояние между выделенной парой вершин или определить кратчайший путь между ними. Если граф несвязен, то может потребоваться найти все его компоненты. В нашем курсе строятся алгоритмы для решения этих и других подобных вопросов.