Сведение решения матричной игры к решению пары
двойственных задач линейного программирования
Подставляя (12.5) в (12.8) и учитывая (12.9), устанавливаем справедливость следующих
неравенств:
 |
(
12.10)
|
Приняв, что цены на продукцию всех типов и запасы сырья всех
видов являются единичными, т.е.
 |
(
12.11)
|
приводим (12.10) к виду:
 |
(
12.12)
|
Введя нормированные переменные
 |
(
12.13)
|
и составленные из них векторы-столбцы
перепишем (12.12) как
или
 |
(
12.14)
|
При этом предполагается, что суммы из знаменателей правых частей равенств
в (12.13) являются
положительными. Это допущение не противоречит условиям

,
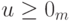
из (12.10). Таким образом,
или (11.15))
 |
(
12.15)
|
Предположим, что общее значение минимакса и максимина ядра, указанное
в (12.9), является положительным. Обозначим обратное ему число через v, т.е.
 |
(
12.16)
|
Заметим, что эти записи учитывают также условия (12.11).
Теперь из (12.13) и (12.16) следует, что
 |
(
12.17)
|
Умножая (12.14) на положительное число v, используя
обозначения (12.17) и учитывая (12.15), выводим справедливость отношений
 |
(
12.18)
|
 |
(
12.19)
|
Из (11.19) и (12.18), (12.19) следует, что пара (x*,y*)
является равновесной (по Нэшу) в смешанном расширении
конечной антагонистической игры с матрицей A. При этом введенное
выше положительное число v оказывается ценой этой игры
в смешанных стратегиях.
Рассмотрим произвольную  матрицу A
с коэффициентами aij,
матрицу A
с коэффициентами aij,  ,
,  , и сопоставим ей вспомогательную
, и сопоставим ей вспомогательную  матрицу C с положительными коэффициентами
матрицу C с положительными коэффициентами
 |
(
12.20)
|
вида (12.1)
при единичных коэффициентах из (12.11)
заведомо
имеет решение.
Действительно, условия

, имеющие вид
 |
(
12.21)
|
определяют
непустую область в
Rn, поскольку
вектор w=0n удовлетворяет этим условиям. В указанной области линейная
форма
(cT,w) оказывается
ограниченной сверху,
ибо, согласно (12.21),
Таким образом, для
линейной программы с матрицей

неравенства
вида (12.8) и вытекающие из них отношения
аналогичные утверждениям (12.18), (12.19),
являются справедливыми при
любой
заданной матрице
A.
Лемма 2.2. Антагонистическая игра с ядром (11.18), соответствующим произвольной  матрице
матрице  и
связанная с ней антагонистическая игра с ядром
и
связанная с ней антагонистическая игра с ядром
 |
(
12.22)
|
(10.20),
имеют одно и то же множество ситуаций равновесия. При этом
где
vc есть цена
смешанного расширения игры
с матрицей
C, а
v - цена
смешанного расширения
игры с матрицей
A.
Доказательство. Как следует из (11.15), (11.18)
и (12.20), (12.22)
где
M(x,y) есть
ядро смешанного расширения антагонистической
игры с матрицей
A. При этом
 |
(
12.23)
|
Следовательно, справедливость отношений
 |
(
12.24)
|
для игры с матрицей
C влечет справедливость аналогичных
отношений (11.19) для игры с матрицей
A, ибо последние выводятся из (12.24)
путем вычитания числа
a из всех частей содержащихся в (12.24)
неравенств.
Доказательство леммы завершается выводом равенства
 |
(
12.25)
|
вытекающего из (12.23).
Итак, мы установили, что при любой  матрице A смешанное
расширение антагонистической игры с вспомогательной
матрицей C из (12.20)
всегда имеет равновесное решение (x*,y*),
которое является равновесным решением также и для исходной
антагонистической игры. Таким образом, мы установили справедливость
следующей теоремы.
матрице A смешанное
расширение антагонистической игры с вспомогательной
матрицей C из (12.20)
всегда имеет равновесное решение (x*,y*),
которое является равновесным решением также и для исходной
антагонистической игры. Таким образом, мы установили справедливость
следующей теоремы.
Теорема 2.3. Матричная игра с произвольной  матрицей A всегда
имеет ситуацию равновесия (по Нэшу) в смешанных
стратегиях
матрицей A всегда
имеет ситуацию равновесия (по Нэшу) в смешанных
стратегиях  ,
,  , которые
могут быть определены из решения (u*,w*) следующей пары
двойственных задач линейного программирования
, которые
могут быть определены из решения (u*,w*) следующей пары
двойственных задач линейного программирования
где a из (12.20).
При этом
Пример 2.7. Рассмотрим численный пример, которому соответствуют рассмотренные
выше матрицы:
Заметим, что вторая
матрица соответствует значению
a=5.
Первая из двух линейных программ, указанных в условиях теоремы, имеет вид:
и ей соответствует решение
найденное симплекс- методом
4.
Следовательно,







 ,
, 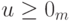 из (12.10). Таким образом,
из (12.10). Таким образом,





 матрицу A
с коэффициентами aij,
матрицу A
с коэффициентами aij,  ,
,  , и сопоставим ей вспомогательную
, и сопоставим ей вспомогательную  матрицу C с положительными коэффициентами
матрицу C с положительными коэффициентами

 , имеющие вид
, имеющие вид

 неравенства
вида (12.8) и вытекающие из них отношения
неравенства
вида (12.8) и вытекающие из них отношения
 матрице
матрице  и
связанная с ней антагонистическая игра с ядром
и
связанная с ней антагонистическая игра с ядром





 матрице A смешанное
расширение антагонистической игры с вспомогательной
матрицей C из (12.20)
всегда имеет равновесное решение (x*,y*),
которое является равновесным решением также и для исходной
антагонистической игры. Таким образом, мы установили справедливость
следующей теоремы.
матрице A смешанное
расширение антагонистической игры с вспомогательной
матрицей C из (12.20)
всегда имеет равновесное решение (x*,y*),
которое является равновесным решением также и для исходной
антагонистической игры. Таким образом, мы установили справедливость
следующей теоремы. матрицей A всегда
имеет ситуацию равновесия (по Нэшу) в смешанных
стратегиях
матрицей A всегда
имеет ситуацию равновесия (по Нэшу) в смешанных
стратегиях  ,
,  , которые
могут быть определены из решения (u*,w*) следующей пары
двойственных задач линейного программирования
, которые
могут быть определены из решения (u*,w*) следующей пары
двойственных задач линейного программирования






